题目内容
 如图,在长方形ACDF中,AC=DF,点B在CD上,点E在DF上,BC=DE=a,AC=BD=b,AB=BE=c,且AB⊥BE.
如图,在长方形ACDF中,AC=DF,点B在CD上,点E在DF上,BC=DE=a,AC=BD=b,AB=BE=c,且AB⊥BE.(1)用两种不同的方法表示长方形ACDF的面积S
方法一:S=
ab+b2
ab+b2
方法二:S=
ab+
b2-
a2+
c2.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
ab+
b2-
a2+
c2.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)求a,b,c之间的等量关系(需要化简)
(3)请直接运用(2)中的结论,求当c=5,a=3,S的值.
分析:(1)方法一,根据矩形的面积公式就可以直接表示出S;
方法二,根据矩形的面积等于四个三角形的面积之和求出结论即可;
(2)根据方法一与方法二的S相等建立等式就可以表示出a,b,c之间的等量关系;
(3)先由(2)的结论求出b的值,然后代入S的解析式就可以求出结论.
方法二,根据矩形的面积等于四个三角形的面积之和求出结论即可;
(2)根据方法一与方法二的S相等建立等式就可以表示出a,b,c之间的等量关系;
(3)先由(2)的结论求出b的值,然后代入S的解析式就可以求出结论.
解答:解:(1)由题意,得
方法一:S1=b(a+b)=ab+b2
方法二:S2=
ab+
ab+
(b-a)(b+a)+
c2,
=ab+
b2-
a2+
c2.
(2)∵S1=S2,
∴ab+b2=ab+
b2-
a2+
c2,
∴2ab+2b2=2ab+b2-a2+c2,
∴a2+b2=c2.
(3)∵a2+b2=c2.且c=5,a=3,
∴b=4,
∴S=3×4+16
=28.
答:S的值为28.
故答案为:ab+b2,ab+
b2-
a2+
c2.
方法一:S1=b(a+b)=ab+b2
方法二:S2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=ab+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵S1=S2,
∴ab+b2=ab+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴2ab+2b2=2ab+b2-a2+c2,
∴a2+b2=c2.
(3)∵a2+b2=c2.且c=5,a=3,
∴b=4,
∴S=3×4+16
=28.
答:S的值为28.
故答案为:ab+b2,ab+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了整式的混合运算的运用,矩形的面积公式的运用,三角形的面积公式的运用,化简求值的运用.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
 如图,在长方形ABCD中,E是AD的中点,F是CE的中点,若△BDF的面积为6平方厘米,则长方形ABCD的面积是
如图,在长方形ABCD中,E是AD的中点,F是CE的中点,若△BDF的面积为6平方厘米,则长方形ABCD的面积是 如图,在长方形ABCD中,DC=5cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC边上,设此点为F,若△ABF的面积为30cm2,求折叠△AED的面积.
如图,在长方形ABCD中,DC=5cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC边上,设此点为F,若△ABF的面积为30cm2,求折叠△AED的面积. 如图,在长方形ABCD中,放入6个形状和大小都相同的小长方形,已知小长方形的长为a,宽为b,且a>b.
如图,在长方形ABCD中,放入6个形状和大小都相同的小长方形,已知小长方形的长为a,宽为b,且a>b.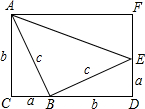 如图,在长方形ACDF中,AC=DF,点B在CD上,点E在DF上,BC=DE=a,AC=BD=b,AB=BE=c,且AB⊥BE.
如图,在长方形ACDF中,AC=DF,点B在CD上,点E在DF上,BC=DE=a,AC=BD=b,AB=BE=c,且AB⊥BE.