题目内容
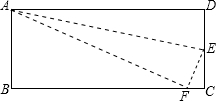 如图,在长方形ABCD中,DC=5cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC边上,设此点为F,若△ABF的面积为30cm2,求折叠△AED的面积.
如图,在长方形ABCD中,DC=5cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC边上,设此点为F,若△ABF的面积为30cm2,求折叠△AED的面积.
分析:根据三角形的面积求得BF的长,再根据勾股定理求得AF的长,即为AD的长;设DE=x,则EC=5-x,EF=x.根据勾股定理列方程求得x的值,进而求得△AED的面积.
解答:解:由折叠的对称性,得AD=AF,DE=EF.
由S△ABF=
BF•AB=30,AB=5,
得BF=12.
在Rt△ABF中,由勾股定理,得
AF=
=13.
所以AD=13.
设DE=x,则EC=5-x,EF=x,FC=1,
在Rt△ECF中,EC2+FC2=EF2,
即(5-x)2+12=x2.
解得x=
.
故S△ADE=
AD•DE=
×13×
=16.9(cm2).
由S△ABF=
| 1 |
| 2 |
得BF=12.
在Rt△ABF中,由勾股定理,得
AF=
| AB2+BF2 |
所以AD=13.
设DE=x,则EC=5-x,EF=x,FC=1,
在Rt△ECF中,EC2+FC2=EF2,
即(5-x)2+12=x2.
解得x=
| 13 |
| 5 |
故S△ADE=
| 1 |
| 2 |
| 1 |
| 2 |
| 13 |
| 5 |
点评:此题主要是能够根据轴对称的性质得到相等的线段,能够熟练根据勾股定理列方程求得未知的线段.

练习册系列答案
相关题目
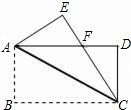 于点F.
于点F. 如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长.
如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长.

