题目内容
已知实数a,b满足a2+3a-1=0,b2+3b-1=0(a≠b),则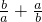 的值为
的值为
- A.2
- B.-9
- C.-11
- D.11
C
分析:把a、b看作一元二次方程x2+3x-1=0的两个根,然后根据根与系数的关系求出a+b、ab的值,再把所求算式通分整理后代入数据进行计算即可得解.
解答:∵实数a,b满足a2+3a-1=0,b2+3b-1=0(a≠b),
∴a、b可以看作是方程x2+3x-1=0的两个根,
∴a+b=-3,ab=-1,
 +
+ =
= =
= =
= =-11.
=-11.
故选C.
点评:本题考查了根与系数的关系,把a、b看作方程x2+3x-1=0的两个根,利用根与系数的关系求出a+b与ab的值是解题的关键,也是本题的突破点.
分析:把a、b看作一元二次方程x2+3x-1=0的两个根,然后根据根与系数的关系求出a+b、ab的值,再把所求算式通分整理后代入数据进行计算即可得解.
解答:∵实数a,b满足a2+3a-1=0,b2+3b-1=0(a≠b),
∴a、b可以看作是方程x2+3x-1=0的两个根,
∴a+b=-3,ab=-1,
 +
+ =
= =
= =
= =-11.
=-11.故选C.
点评:本题考查了根与系数的关系,把a、b看作方程x2+3x-1=0的两个根,利用根与系数的关系求出a+b与ab的值是解题的关键,也是本题的突破点.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
已知实数a、b满足a<b,则下列式子中正确的是( )
A、
| ||||
| B、b-a>0 | ||||
| C、a2<b2 | ||||
| D、a4<b4 |