题目内容
如图，点A为⊙O外一点，射线AB、AC分别切⊙O于B、C两点，若∠A=60°，则∠BOC=________．
120°
分析：根据切线的性质可得∠ABO=∠ACO=90°，已知∠A=60°，根据四边形内角和即可求解．
解答：∵射线AB、AC分别切⊙O于B、C两点，
∴∠ABO=∠ACO=90°，
∵∠A=60°，
∴∠BOC=360°-90°-90°-60°=120°．
故答案为：120°．
点评：考查了切线的性质：圆的切线垂直于经过切点的半径和四边形内角和为360°．
分析：根据切线的性质可得∠ABO=∠ACO=90°，已知∠A=60°，根据四边形内角和即可求解．
解答：∵射线AB、AC分别切⊙O于B、C两点，
∴∠ABO=∠ACO=90°，
∵∠A=60°，
∴∠BOC=360°-90°-90°-60°=120°．
故答案为：120°．
点评：考查了切线的性质：圆的切线垂直于经过切点的半径和四边形内角和为360°．
练习册系列答案
相关题目
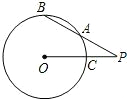如图，点P是⊙O外一点，PAB为⊙O的一条割线，且PA=AB，PO交⊙O于点C，若OC=3，OP=5，则AB长为（ ）A、
| ||
B、2
| ||
C、
| ||
D、
|
已知：如图①，点C为线段AB上一点，△ACM和△CBN都是等边三角形，AN，BM交于点P，则△BCM≌△NCA，易证结论：①BM=AN．
如图，点P为⊙O外一点，PO及延长线分别交⊙O于A、B，过点P作一直线交⊙O于M、N（异于A、B）．求证：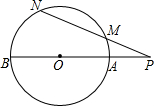
如图，点P为⊙O外一点，PO及延长线分别交⊙O于A、B，过点P作一直线交⊙O于M、N（异于A、B）．求证：
