题目内容
如图(1),在直角坐标系xoy中,抛物线![]() 与x轴交于A、B两点,交y轴于点C,过A点的直线与抛物线的另一交点为D(m,3),与y轴相交于点E,
与x轴交于A、B两点,交y轴于点C,过A点的直线与抛物线的另一交点为D(m,3),与y轴相交于点E,
点A的坐标为(![]() ,0),∠BAD=
,0),∠BAD=![]() ,点P是抛物线上的一点,且点P在第一象限.
,点P是抛物线上的一点,且点P在第一象限.
(1)求直线AD和抛物线的解析式;
 (2)若
(2)若![]()
![]() ,求点P的坐标.
,求点P的坐标.
(3)如图(2),若![]() 为抛物线的顶点,点
为抛物线的顶点,点![]() 为
为
![]() 轴上一点,求使
轴上一点,求使![]() 最小时,点
最小时,点![]() 的
的
坐标,并求![]() 的最小值.
的最小值.
解:(1)在Rt![]() 中
中
AO=1,![]()
![]()
![]() E(0,1)
E(0,1)
设直线AD的方程为![]() ,
,
把A(-1,0),E(0,1)代入![]() 中,得
中,得
![]() 解得
解得![]()
![]() 直线AD的方程为:
直线AD的方程为:![]() ……2分
……2分
令![]() ,解得
,解得![]()
![]() D(2,3)
D(2,3)
把![]() A(-1,0),D(2,3)代入
A(-1,0),D(2,3)代入![]() 中,得
中,得
![]() 解得
解得![]()
![]() 抛物线的
抛物线的![]() 方程为:
方程为:![]() ……4分
……4分
(2)![]()
![]()
![]() ……5分
……5分
设P点坐标为(![]() ,
,![]() ),
),
过P点作![]() 交AB于点F,交AD于点H,则H(
交AB于点F,交AD于点H,则H(![]() ,
,![]() )
)
![]()
![]()
![]()
![]()
解得:![]() ,
,![]() ……7分
……7分
![]() 点P的坐标为(1,4),(2,3) ……8分
点P的坐标为(1,4),(2,3) ……8分
(3)M(1,4),B(3,0)
点M关于y轴的对称点为M’(—1,4) ……9分
直线BM’的方程为![]() ……10分
……10分
令![]() ,解得
,解得![]()
![]() 点Q的坐标为(0,3) ……11分
点Q的坐标为(0,3) ……11分
![]()
![]() 的最小值为BM’=
的最小值为BM’= ![]() ……12分
……12分

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 23、在数学上,为了确定平面上点的位置,我们常用下面的方法:如图甲,在平面内画两条互相垂直,并且有公共原点O的数轴,通常一条画成水平,叫x轴,另一条画成铅垂,叫y轴,这样,我们就说在平面上建立了一个平面直角坐标系,这是由法国数学家和哲学家笛卡尔创立的,这样我们就能确定平面上点的位置,例如,要确定点M的位置,只要作MP⊥x轴,MP⊥y轴,设垂足N,P在各自数轴上所表示的数分别为x,y,则x叫做点M的横坐标,y叫做点M的纵坐标,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),(1)△ABC在平面直角坐标系中的位置如图乙,请把△ABC向右平移3个单位,在平面直角坐标系中画出平移后的△A′B′C′;
23、在数学上,为了确定平面上点的位置,我们常用下面的方法:如图甲,在平面内画两条互相垂直,并且有公共原点O的数轴,通常一条画成水平,叫x轴,另一条画成铅垂,叫y轴,这样,我们就说在平面上建立了一个平面直角坐标系,这是由法国数学家和哲学家笛卡尔创立的,这样我们就能确定平面上点的位置,例如,要确定点M的位置,只要作MP⊥x轴,MP⊥y轴,设垂足N,P在各自数轴上所表示的数分别为x,y,则x叫做点M的横坐标,y叫做点M的纵坐标,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),(1)△ABC在平面直角坐标系中的位置如图乙,请把△ABC向右平移3个单位,在平面直角坐标系中画出平移后的△A′B′C′;
 的图象与边BC交于点F.
的图象与边BC交于点F.
 .且
.且 ,求k的值.
,求k的值.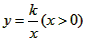 的图象与边BC交于点F。
的图象与边BC交于点F。