题目内容
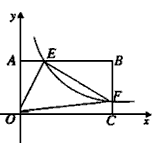
如图，将-矩形OABC放在直角坐际系中，O为坐标原点，点A在x轴正半轴上，点E是边AB上的一个动点（不与点A、N重合），过点E的反比例函数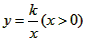
的图象与边BC交于点F。
（1）若△OAE、△OCF的而积分别为S1，S2，且S1+S2=2，求k的值；
（2）若OA=2，0C=4，问当点E运动到什么位置时，四边形OAEF的面积最大．其最大值为多少？
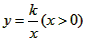的图象与边BC交于点F。（1）若△OAE、△OCF的而积分别为S1，S2，且S1+S2=2，求k的值；
（2）若OA=2，0C=4，问当点E运动到什么位置时，四边形OAEF的面积最大．其最大值为多少？
解：（1）∵点E、F在函数
的图象上，
∴设
， 
∴
，
∵
，
∴
，k=2；
（2）∵四边形OABC为矩形，OA=2，OC=4，
设
，
∴BE=
，BF=
∴
∵
，
∴
=
∴当k=4时，
，
∴AE=2，
当点E运动到AB的中点时，四边形OAEF的面积最大，最大值是5。
的图象上， ∴设
， ∴
，∵
，∴
，k=2；（2）∵四边形OABC为矩形，OA=2，OC=4，
设
， ∴BE=
，BF= ∴
∵
， ∴
=
∴当k=4时，
，∴AE=2，
当点E运动到AB的中点时，四边形OAEF的面积最大，最大值是5。
练习册系列答案
津桥教育计算小状元系列答案
相关题目
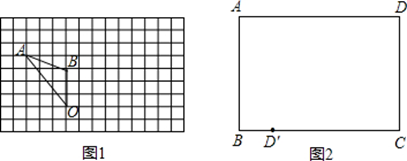
如图，平面直角坐标系中，已知矩形OABC，O为原点，点A、C分别在x轴、y轴上，点B的坐标为（1，2），连接OB，将△OAB沿直线OB翻折，点A落在点D的位置．则点D的坐标为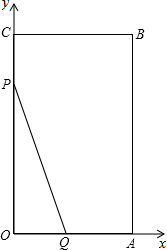
已知：在平面直角坐标系中矩形OABC如图，且A（6，0）、C（0，10），P点从C出发沿折线COA匀速运动、Q点从O出发沿折线OAB匀速运动，P、Q两点同时出发运动t秒，且速度均为每秒2个单位长度，设S△OPQ=S．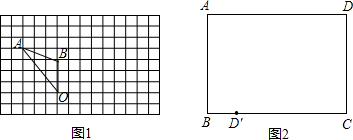
秒，且速度均为每秒2个单位长度,设
.
平分矩形OABC面积，求
的值；（经验之谈：过对称中心的任意一条直线均可将中心对称图形分成面积相等的两部分.）
，
