题目内容
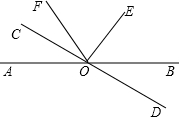
 已知直线AB、CD、EF相交于点O,∠1:∠3=3:1,∠2=20°,求∠DOE的度数.
已知直线AB、CD、EF相交于点O,∠1:∠3=3:1,∠2=20°,求∠DOE的度数.
解:∵∠1:∠3=3:1,
∴设∠1=3k,∠3=k,
则3k+20°+k=180°,
解得k=40°,
∴∠1=3k=120°,
∴∠COF=∠1+∠2=120°+20°=140°,
∠DOE=∠COF=140°.
故答案为:140°.
分析:根据∠1:∠3=3:1设出∠1与∠3,再根据∠1、∠2、∠3的和等于180°列式求出∠1的度数,然后再求出∠1与∠2的和,再根据对顶角相等求解即可.
点评:本题考查了对顶角相等的性质,平角等于180°,根据比例式设出∠1与∠3是并求出∠1的度数是解题的关键.
∴设∠1=3k,∠3=k,
则3k+20°+k=180°,
解得k=40°,
∴∠1=3k=120°,
∴∠COF=∠1+∠2=120°+20°=140°,
∠DOE=∠COF=140°.
故答案为:140°.
分析:根据∠1:∠3=3:1设出∠1与∠3,再根据∠1、∠2、∠3的和等于180°列式求出∠1的度数,然后再求出∠1与∠2的和,再根据对顶角相等求解即可.
点评:本题考查了对顶角相等的性质,平角等于180°,根据比例式设出∠1与∠3是并求出∠1的度数是解题的关键.

练习册系列答案
相关题目
 如图,已知直线AB和CD相交于O点,∠DOE是直角,OF平分∠AOE,∠BOD=22°,求∠COF的度数.
如图,已知直线AB和CD相交于O点,∠DOE是直角,OF平分∠AOE,∠BOD=22°,求∠COF的度数. 2、如图,已知直线AB与CD相交于O,EO⊥CD,垂足为O,则图中∠AOE和∠DOB的关系是( )
2、如图,已知直线AB与CD相交于O,EO⊥CD,垂足为O,则图中∠AOE和∠DOB的关系是( ) 24、如图所示,已知直线AB,CD被直线EF所截,如果∠BMN=∠DNF,∠1=∠2,那么MQ∥NP.为什么?
24、如图所示,已知直线AB,CD被直线EF所截,如果∠BMN=∠DNF,∠1=∠2,那么MQ∥NP.为什么? 如图,已知直线AB,CD,EF相交于点O,若∠AOC=50°,则∠COB的度数等于
如图,已知直线AB,CD,EF相交于点O,若∠AOC=50°,则∠COB的度数等于 如图,已知直线AB和CD相交于O点,∠COE=90°,OF平分∠AOE,∠COF=34°,求∠AOC的度数.
如图,已知直线AB和CD相交于O点,∠COE=90°,OF平分∠AOE,∠COF=34°,求∠AOC的度数.