题目内容
如图,四边形ABCD是菱形,对角线AC与BD交于点O,且AC=80,BD=60.动点M,N分别以每秒1个单位的速度从点A,D同时出发,分别沿A→O→D和D→A运动,当点N到达点A时,M,N同时停止运动.设运动时间为t秒.
(1)求菱形ABCD的周长.
(2)设△DMN的面积为S,求S关于t的解析式,并求S的最大值(提示:需分两种情况讨论).


【考点】四边形综合题.
【分析】(1)根据勾股定理及菱形的性质,求出菱形的周长;
(2)在动点M、N运动过程中:①当0<t≤40时,如答图1所示,②当40<t≤50时,如答图2所示.分别求出S的关系式,然后利用二次函数的性质求出最大值.
【解答】解:(1)在菱形ABCD中,
∵四边形ABCD是菱形,对角线AC与BD交于点O,且AC=80,BD=60,
∴OA=40,OD=30,
∵AC⊥BD,
∴AD=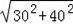
 =50.
=50.
∴菱形ABCD的周长为200.
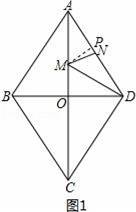
(2)过点M作MP⊥AD,垂足为点P.
①当0<t≤40时,如图1,

∵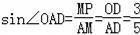
 ,
,
∴MP=AM•sin∠OAD=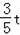
 .
.
∴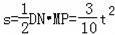
 .
.
∵S随t的增大而增大,
∴当t=40时,最大值为480;
②当40<t≤50时,如图2,
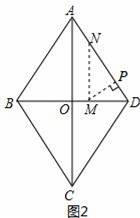

∴MD=80﹣t.
∵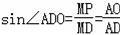
 ,
,
∴MP=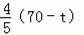
 .
.
∴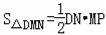
 =
=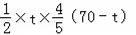
 =
=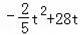
 =
=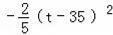
 +490.
+490.
∵S随t的增大而减小,
∴当t=40时,最大值为480.
综上所述,S的最大值为480.
【点评】本题考查了菱形的性质、勾股定理、解直角三角形、二次函数极值等知识点,涉及考点较多,有一定的难度.第(2)问中,动点M在线段AO和OD上运动时,是两种不同的情形,需要分类讨论;

练习册系列答案
相关题目
 学生用于课外作业的平均时间,从该班学生中随机抽取了10名学生进行调查,得到他们用于课外作业的时间(单位:min)如下:75,80,85,65,95,80,85,85,80,90.由此估计该班的学生用于课外作业的平均时间是
学生用于课外作业的平均时间,从该班学生中随机抽取了10名学生进行调查,得到他们用于课外作业的时间(单位:min)如下:75,80,85,65,95,80,85,85,80,90.由此估计该班的学生用于课外作业的平均时间是
 •cos60°﹣(π+2015)0.
•cos60°﹣(π+2015)0.
 .
.
 有意义,则x的取值是( )
有意义,则x的取值是( )
 .
.