题目内容
15.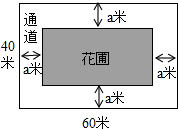 如图,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.
如图,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.(1)用含a的式子表示花圃的面积;
(2)如果通道所占面积是整个长方形空地面积的$\frac{3}{8}$,求出此时通道的宽;
(3)若按上述要求施工,同时校长希望长方形花圃的形状与原长方形空地的形状相似,聪明的你想一想能不能满足校长的要求?若能,求出此时通道的宽;若不能,则说明理由.
分析 (1)用含a的式子先表示出花圃的长和宽后利用其矩形面积公式列出式子即可;
(2)根据通道所占面积是整个长方形空地面积的$\frac{3}{8}$,列出方程进行计算即可;
(3)根据题意得:$\frac{40-2a}{60-2a}$=$\frac{40}{60}$,求得a值后即可判定是否满足要求.
解答 解:(1)由图可知,花圃的面积为(40-2a)(60-2a);
(2)由已知可列式:60×40-(40-2a)(60-2a)=$\frac{3}{8}$×60×40,
解以上式子可得:a1=5,a2=45(舍去),
答:所以通道的宽为5米;
(3)假设能满足要求,则$\frac{40-2a}{60-2a}$=$\frac{40}{60}$,
解得:a=0,
因为a=0不符合实际情况,所以不能满足其要求.
点评 本题考查了及一元二次方程的应用,解题的关键是表示出花圃的长和宽.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
5.下列各组中的两个项不属于同类项的是( )
| A. | 3x2y和-2x2y | B. | -xy和2yx | C. | 23和32 | D. | a2b和ab2 |
7.下列各对数中,互为相反数的是( )
| A. | -(-2)3与|-2|3 | B. | (-2)3与-23 | C. | -22与+(-2)2 | D. | -(-2)与|-2| |
4.下列语句不是命题的是( )
| A. | 亮亮同学是初三(甲)班的学生 | |
| B. | 2是质数 | |
| C. | 不知道亮亮今天数学作业做完了没有 | |
| D. | 如果a>b,a>c,那么b>c |