Question

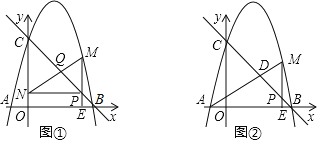
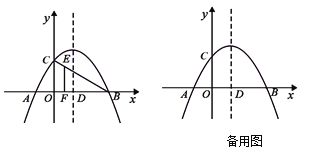
【题目】如图，在平面直角坐标系中，二次函数的图像与x轴交于点A，B，与y轴交于点C，其对称轴与x轴交于点D．

（1）求二次函数的解析式及其对称轴；

（2）若点E是线段BC上的一点，过点E作x轴的垂线，垂足为F，且EF=2EC，求点E的坐标；

（3）若点P是抛物线对称轴上的一个动点，连接PA，PC，设点P的纵坐标为t，当∠APC不小于60°时，求t的取值范围．

Answer 1

【答案】（1），对称轴为：直线；（2）；（3）0≤t≤2．

【解析】

（1）将A,B两点坐标代入到二次函数解析式中进行求解；

（2）有多种方法进行求解，如根据△BFF∽△BCO，求出EF的长度，即求出E点纵坐标，将E点纵坐标代入到BC直线解析式后，求出其横坐标即可得到E点坐标.

(3)引入圆，分点圆上，内，外进行分析.

（1）将A(，0)，B(，0)代入得

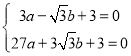
解得，∴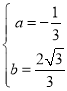

对称轴为：直线．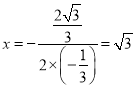

（2）如图所示．

∵CO⊥x轴，EF⊥x轴，

∴CO//EF.

∴△BEF∽△BCO.

∴.

设EC=m，则EF=2m.

由B(，0)，C(0，3)得BC=.

∴．

解得.

∴．

又由得，∴OF==．

∴

解法二：由B(，0)，C(0，3)得BC=，∴∠OBC=30，

设EC=m，则EF=2m，EB=6－m.

∴，解得.

∴.

利用三角函数求得BF=EF÷tan 30°=，∴OF==

∴

解法三：求出后，即E点的纵坐标为，

由B(，0)，C(0，3)得直线BC解析式为，

将yE=代入得xE=，∴(解法二、解法三参考解法一相应步骤给分)

（3）如图2，由题意知∠CAO=60

作∠CAO的平分线AQ，交y轴于Q

则∠QAC=∠QCA=30

∴∠AQC=120

以Q为圆心，QA为半径作圆，与抛物线对称轴交于点M1，M2

当点M在圆上时，则∠AM1C=∠AM2C=∠AQC=60．

当点M在圆内时，∠AMC＞60，

当点M在圆外时，∠AMC＜60，

过Q作QH垂直于对称轴．在Rt△AOQ中，求得AQ=2，

在Rt△M1QH中，M1H=

∴M1D=1+1=2，M2D=1－1=0

∴0≤t≤2．