题目内容
小明用下面的方法求出方程 的解,请你仿照他的方法求出下面另外两个方程的解,并把你的解答过程填写在下面的表格中.
的解,请你仿照他的方法求出下面另外两个方程的解,并把你的解答过程填写在下面的表格中.
| 方程 | 换元法得新方程 | 解新方程 | 检验 | 求原方程的解 |
 | 令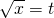 , ,则3t-5=0 | 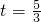 |  |  , ,∴  . . |
 | ________ | ________ | ________ | ________ |
 | ________ | ________ | ________ | ________ |
令 =t,
=t,
则t2-2t-3=0 t1=3,t2=-1, t1=3>0,t2=-1<0, =3,
=3,
∴x=9. 令 =t,
=t,
则t2+t=2 t1=-2,t2=1 t1=-2<0,t2=1>0 =1,
=1,
∴x=3.
分析:令 =t,则t2-2t-3=0,求出t的值,再进行检验;令
=t,则t2-2t-3=0,求出t的值,再进行检验;令 =t,则t2+t=2,求出t的值,再进行检验,最后求出x的值即可.
=t,则t2+t=2,求出t的值,再进行检验,最后求出x的值即可.
解答:x-2 -3=0,
-3=0,
令 =t,
=t,
则t2-2t-3=0,
解得:t1=3,t2=-1,
检验:∵t1=3>0,t2=-1<0(舍去),
∴ =3,
=3,
x=9;
x+ -2=2,
-2=2,
令 =t,
=t,
则t2+t=2,
解得:t1=-2,t2=1,
检验:t1=-2<0(舍去),t2=1>0,
∴ =1,
=1,
x-2=1,
x=3,
故答案为:令 =t,则t2-2t-3=0,t1=3,t2=-1,t1=3>0,t2=-1<0,
=t,则t2-2t-3=0,t1=3,t2=-1,t1=3>0,t2=-1<0, =3,∴x=9;令
=3,∴x=9;令 =t,则t2+t=2,t1=-2,t2=1,t1=-2<0,t2=1>0,
=t,则t2+t=2,t1=-2,t2=1,t1=-2<0,t2=1>0, =1,∴x=3.
=1,∴x=3.
点评:本题考查了解无理方程和解有理方程,关键是能把无理方程转化成有理方程,注意:解无理方程一定要进行检验.
 =t,
=t,则t2-2t-3=0 t1=3,t2=-1, t1=3>0,t2=-1<0,
 =3,
=3,∴x=9. 令
 =t,
=t,则t2+t=2 t1=-2,t2=1 t1=-2<0,t2=1>0
 =1,
=1,∴x=3.
分析:令
 =t,则t2-2t-3=0,求出t的值,再进行检验;令
=t,则t2-2t-3=0,求出t的值,再进行检验;令 =t,则t2+t=2,求出t的值,再进行检验,最后求出x的值即可.
=t,则t2+t=2,求出t的值,再进行检验,最后求出x的值即可.解答:x-2
 -3=0,
-3=0,令
 =t,
=t,则t2-2t-3=0,
解得:t1=3,t2=-1,
检验:∵t1=3>0,t2=-1<0(舍去),
∴
 =3,
=3,x=9;
x+
 -2=2,
-2=2,令
 =t,
=t,则t2+t=2,
解得:t1=-2,t2=1,
检验:t1=-2<0(舍去),t2=1>0,
∴
 =1,
=1,x-2=1,
x=3,
故答案为:令
 =t,则t2-2t-3=0,t1=3,t2=-1,t1=3>0,t2=-1<0,
=t,则t2-2t-3=0,t1=3,t2=-1,t1=3>0,t2=-1<0, =3,∴x=9;令
=3,∴x=9;令 =t,则t2+t=2,t1=-2,t2=1,t1=-2<0,t2=1>0,
=t,则t2+t=2,t1=-2,t2=1,t1=-2<0,t2=1>0, =1,∴x=3.
=1,∴x=3.点评:本题考查了解无理方程和解有理方程,关键是能把无理方程转化成有理方程,注意:解无理方程一定要进行检验.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
小明用下面的方法求出方程2
-3=0的解,请你仿照他的方法求出下面另外两个方程的解,并把你的解答过程填写在下面的表格中.
| x |
| 方程 | 换元法得新方程 | 解新方程 | 检验 | 求原方程的解 | ||||||||||||||
2
|
令
则2t-3=0 |
t=
|
t=
|
所以x=
| ||||||||||||||
x+2
|
||||||||||||||||||
x+
|
小明用下面的方法求出方程2
-4=0的解,请你仿照他的方法求出下面另外两个方程的解,并把你的解答过程填写在下面的表格中.
| x |
| 方程 | 换元法得新方程 | 解新方程 | 检验 | 求原方程的解 | ||||||
2
|
令
则2t-4=0 |
t=2 | t=2>0 |
所以x=4 | ||||||
x+2
|
||||||||||
x+
|