题目内容
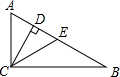如图，在Rt△ABC，∠ACB=90°，CD、CE是斜边上的高和中线，AC=CE=10cm，则BD长为（ ）| A、5cm | B、10cm |
| C、15cm | D、25cm |
考点：等边三角形的判定与性质,含30度角的直角三角形,直角三角形斜边上的中线
专题：
分析：根据条件可求得AC=AE=CE=BE，可证得△ACE为等边三角形，可求得DE=
AE，可求得DE，则可求得BD．
| 1 |
| 2 |
解答：解：
∵∠ACB=90°，CE为斜边上的中线，
∴AE=BE=CE=AC=10cm，
∴△ACE为等边三角形，
∵CD⊥AE，
∴DE=
AE=5cm，
∴BD=DE+BE=5cm+10cm=15cm，
故选C．
∵∠ACB=90°，CE为斜边上的中线，
∴AE=BE=CE=AC=10cm，
∴△ACE为等边三角形，
∵CD⊥AE，
∴DE=
| 1 |
| 2 |
∴BD=DE+BE=5cm+10cm=15cm，
故选C．
点评：本题主要考查直角三角形的性质及等边三角形的性质，根据直角三角形的性质求得BE、根据等边三角形的性质求得DE是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
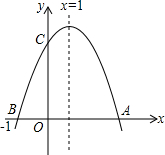如图，二次函数y=ax2+bx+c（a≠0）的图象与x轴交于A、B两点，与y轴交于点C，点B坐标（-1，0），下面的四个结论：①ac＜0；②a+b+c＜0；③b2-4ac＞0；④若（-5，y1），（| 5 |
| 2 |
| A、①③④ | B、②③④ |
| C、②③④ | D、①③ |
如图，是一个正方体的表面展开图，则原正方体中“国”字所在的面相对的面上标的字是|-
|=（ ）
| 2 |
| 11 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
如图，AC为⊙O的直径，B，D为⊙O上的两点，则由A，B，C，D，四点可以构造
如图，在∠1、∠2、∠3中，下列说法正确的是（ ）
| A、有理数和数轴上的点一一对应 | ||||||
| B、立方根等于本身的数只有±1 | ||||||
| C、（-2）2的算术平方根是-2 | ||||||
D、-
|
分别根据下列已知条件，再补充一个条件使得如图所示的△ABD和△ACE全等：