题目内容
 如图,在⊙O中,P为
如图,在⊙O中,P为 的中点,PD⊥CD,CD交⊙O于A,若AC=AD=1,求AB的长.
的中点,PD⊥CD,CD交⊙O于A,若AC=AD=1,求AB的长.
 解:解:连接PC PB PA,过P做BA垂线于H点,
解:解:连接PC PB PA,过P做BA垂线于H点,∵在⊙O中,P为
 的中点,
的中点,∴PB=PC,
∴∠B=∠C,∠PHB=∠PDA,
∴∠BPH=∠DPC,
在△PBH与△PCD中,
 ,
,∴△PBH≌△PCD(ASA),
∴BH=CD=2,PH=PD,
在Rt△PHA与Rt△PDA中,
 ,
,∴Rt△PHA≌Rt△PDA(HL),
∴HA=AD=1
∴AB=BH+HA=3.
分析:接PC PB PA,过P做BA垂线于H点,根据P为
 的中点可知PB=PC,再由全等三角形的判定定理可得出△PBH≌△PCD,Rt△PHA≌Rt△PDA,根据AC=AD=1即可得出结论.
的中点可知PB=PC,再由全等三角形的判定定理可得出△PBH≌△PCD,Rt△PHA≌Rt△PDA,根据AC=AD=1即可得出结论.点评:本题考查的是圆周角定理及全等三角形的判定与性质,根据题意作出辅助线,构造出全等三角形是解答此题的关键.

练习册系列答案
相关题目
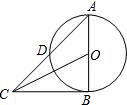 如图,在⊙O中,AB为⊙O的直径,AD为弦,过B点的切线与AD的延长线交于点C,若AD=DC.则sin∠ACO等于( )
如图,在⊙O中,AB为⊙O的直径,AD为弦,过B点的切线与AD的延长线交于点C,若AD=DC.则sin∠ACO等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
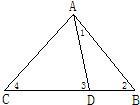 24、如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=4,∠BAC=63°,试求∠DAC,∠ADC的度数.
24、如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=4,∠BAC=63°,试求∠DAC,∠ADC的度数. 16、已知:如图,在?ABCD中,E为AD中点,连接CE并延长交BA的延长线于F.
16、已知:如图,在?ABCD中,E为AD中点,连接CE并延长交BA的延长线于F. 19、已知:如图,在⊙O中,CD为弦,A、B两点在CD的两端延长线上,且AC=BD.
19、已知:如图,在⊙O中,CD为弦,A、B两点在CD的两端延长线上,且AC=BD. 如图,在?ABCD中,E为AB延长线上一点,AB:AE=2:5,若S△CDF=12cm2,则S△BEF=
如图,在?ABCD中,E为AB延长线上一点,AB:AE=2:5,若S△CDF=12cm2,则S△BEF=