题目内容
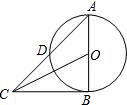 如图,在⊙O中,AB为⊙O的直径,AD为弦,过B点的切线与AD的延长线交于点C,若AD=DC.则sin∠ACO等于( )
如图,在⊙O中,AB为⊙O的直径,AD为弦,过B点的切线与AD的延长线交于点C,若AD=DC.则sin∠ACO等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:连接BD,作OE⊥AD.在Rt△OEC中运用三角函数的定义求解.
解答:
解:连接BD,作OE⊥AD.
AB是直径,则BD⊥AC.
∵AD=CD,
∴△BCD≌△BDA,BC=AB.
BC是切线,点B是切点,
∴∠ABC=90°,即△ABC是等腰直角三角形,∠A=45°,OE=
AO.
由勾股定理得,CO=
OB=
AO,所以sin∠ACO=
=
.

解:连接BD,作OE⊥AD.
AB是直径,则BD⊥AC.
∵AD=CD,
∴△BCD≌△BDA,BC=AB.
BC是切线,点B是切点,
∴∠ABC=90°,即△ABC是等腰直角三角形,∠A=45°,OE=
| ||
| 2 |
由勾股定理得,CO=
| 5 |
| 5 |
| EO |
| CO |
| ||
| 10 |
点评:本题利用了切线的性质,等腰直角三角形的判定和性质,勾股定理,正弦的概念求解.

练习册系列答案
相关题目
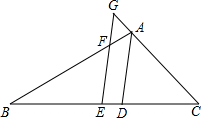 如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于G.
如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于G.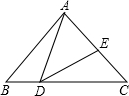 如图,在△ABC中,AB=AC,D为BC边上一点,且∠BAD=30°,若AD=DE,∠EDC=33°,则∠DAE的度数为
如图,在△ABC中,AB=AC,D为BC边上一点,且∠BAD=30°,若AD=DE,∠EDC=33°,则∠DAE的度数为 如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD.
如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD.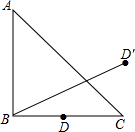 如图,在△ABC中,AB=BC,∠ABC=90°,D是BC的中点,且它关于AC的对称点是D′,BD′=
如图,在△ABC中,AB=BC,∠ABC=90°,D是BC的中点,且它关于AC的对称点是D′,BD′=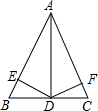 如图,在△ABC中,AB=AC,D点是BC的中点,DE⊥AB于E点,DF⊥AC于F点,则图中全等三角形共有
如图,在△ABC中,AB=AC,D点是BC的中点,DE⊥AB于E点,DF⊥AC于F点,则图中全等三角形共有