��Ŀ����
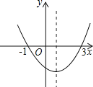
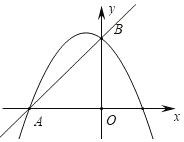
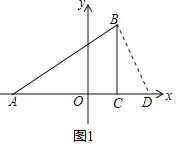
����Ŀ����֪����ͼ����ƽ��ֱ������ϵ�У���ABC��ֱ�������Σ���ACB��90�㣬��A��C������ֱ�ΪA����3��0����C��1��0����tan��BAC��![]() ��
��
��1��д����B�����ꣻ
��2����x������һ��D������BD��ʹ�á�ADB���ABC���ƣ�������ȫ�ȣ��������D�����ꣻ
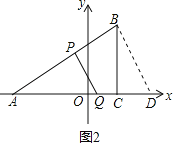
��3���ڣ�2���������£������P�ӵ�A��������2cm/����ٶ���AB���B�˶���ͬʱ��Q�ӵ�D��������1cm/����ٶ���DA���A�˶�����һ����ֹͣ�˶�ʱ����һ����Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt�����Ƿ����������tʹ�á�APQ���ADB���ƣ�����ڣ������t��ֵ���粻���ڣ���˵�����ɣ�
���𰸡���1����B������Ϊ��1��3������2����D������Ϊ��![]() ��0������3�����ڣ���t��
��0������3�����ڣ���t��![]() s��
s��![]() sʱ����APQ���ADB���ƣ�
sʱ����APQ���ADB���ƣ�
��������
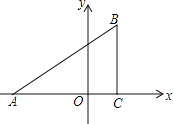
��1���������еĶ������BC���õ���B�����ꣻ
��2�����ݡ�ABC�ס�ADB���õ�![]() =
=![]() ������������AD���õ���D�����ꣻ
������������AD���õ���D�����ꣻ
��3���֡�APQ�ס�ABD����AQP�ס�ABD����������������������ε�������ʽ���㼴�ɣ�
�⣺��1����A����3��0����C��1��0����
��AC��4��
�ߡ�ACB��90�㣬tan��BAC��![]() ��
��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��ã�BC��3��
���B��������1��3����
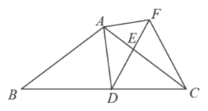
��2����ͼ1����BD��BA��x���ڵ�D��
���ACB����ABD��90�㣬�֡�A����A��
���ABC�ס�ADB��
��![]() ��
��![]() ��
��
��Rt��ABC��AB��![]() ��
��![]() ��5��
��5��
��![]() ��
��![]() ��
��
��ã�AD��![]() ��
��
��OD��AD��AO��![]() ��
��
���D��������![]() ��0����
��0����
��3�����ڣ�
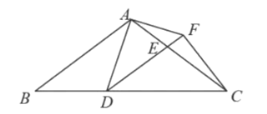
������ã�AP��2t��AQ��![]() ��t��
��t��
��PQ��ABʱ��PQ��BD��
���APQ�ס�ABD��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��ã�t��![]() ��
��
��PQ��ADʱ����AQP����ABD����A����A��
���AQP�ס�ABD��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��ã�t��![]() ��
��
������������t��![]() s��
s��![]() sʱ����APQ���ADB���ƣ�
sʱ����APQ���ADB���ƣ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�