Question

【题目】（概念认识）

若以三角形某边上任意一点为圆心，所作的半圆上的所有点都在该三角形的内部或边上，则将符合条件且半径最大的半圆称为该边关联的极限内半圆．

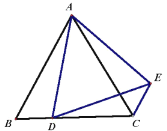
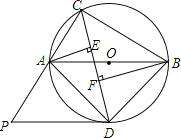
如图①，点P是锐角△ABC的边BC上一点，以P为圆心的半圆上的所有点都在△ABC的内部或边上．当半径最大时，半圆P为边BC关联的极限内半圆．

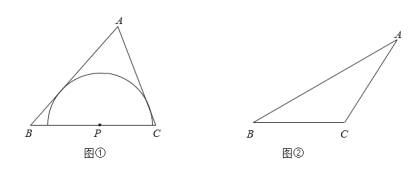
（初步思考）

（1）若等边△ABC的边长为1，则边BC关联的极限内半圆的半径长为 ．

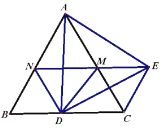
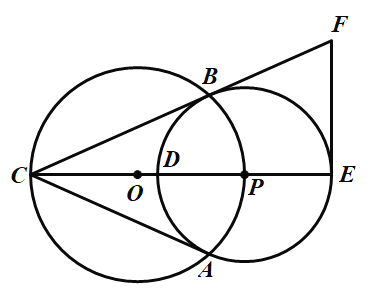
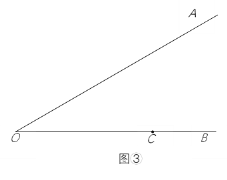
（2）如图②，在钝角△ABC中，用直尺和圆规作出边BC关联的极限内半圆（保留作图痕迹，不写作法）．

（深入研究）

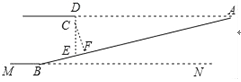
（3）如图③，∠AOB＝30°，点C在射线OB上，OC＝6，点Q是射线OA上一动点．在△QOC中，若边OC关联的极限内半圆的半径为r，当1≤r≤2时，求OQ的长的取值范围．

Answer 1

【答案】（1）；（2）见解析；（3）OQ≥－

【解析】

（1）过P作AB垂线交于D点，根据直角三角形即可得出半径；

（2）过点C作BC的垂线交AB于点D，再作∠BDC的平分线交BC于点P．以点P为圆心，CP为半径在△ABC的内部作半圆即可．

（3）分情况讨论，当r＝1时，OQ取得最小值，设QM＝x，解直角三角形可求得OP=2，,OM=，解Rt△PCN，可得到CN＝．OQ＝OM＋MQ＝＋x，CQ＝CN＋NQ＝＋x，根据S△OPQ∶S△CPQ＝OP∶PC＝1∶2，PM＝PN，得出OQ∶QC＝1∶2，所以QC＝2OQ，则＋x＝2(＋x)，x＝-2，所以OQ＝-．当r＝2时，半圆P经过点C，过点C作OB的垂线交OA于点D．由（2）知，当Q在射线DA上时，OQ4，均符合题意．整合结果可得，当1≤r≤2时，OQ－．

解：（1）如图，过P作AB垂线交于D点，

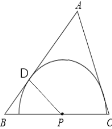
∵△ABC为等边三角形，边长为1，

∴∠DBP=60°，BP= ，

∴R=DP=BP×sin60°=．

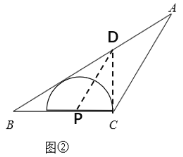
（2）过点C作BC的垂线交AB于点D，再作∠BDC的平分线交BC于

点P．以点P为圆心，CP为半径在△ABC的内部作半圆，如图：

（3）当r＝1时，OQ取得最小值．

如图①，半圆P与OQ、QC分别相切于点M、N，连接PQ．

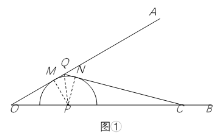
设QM＝x，则QN＝QM＝x．

在Rt△OPM中，∠OMP＝90°，∠AOB＝30°，PM＝1，

∵sin∠AOB＝，tan∠AOB＝，

∴OP＝＝2，OM＝＝．

∴PC＝OC－OP＝4．

在Rt△PCN中，∠PNC＝90°，PN＝1，PC＝4，

∴CN＝＝．

∴OQ＝OM＋MQ＝＋x，CQ＝CN＋NQ＝＋x．

∵S△OPQ∶S△CPQ＝OP∶PC＝1∶2，且PM＝PN，

∴OQ∶QC＝1∶2．

∴QC＝2OQ．

∴＋x＝2(＋x)，

解得x＝-2．

∴OQ＝-2．

当r＝2时，半圆P经过点C．

如图②，过点C作OB的垂线交OA于点D．

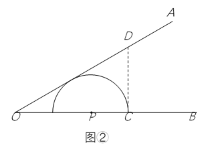
由（2）知，当Q在射线DA上时，OQ4，均符合题意．

∴当1r2时，OQ－．