Question

【题目】如图，已知抛物线的图像经过点，，其对称轴为直线：，过点作轴交抛物线于点，的平分线交线段于点，点是抛物线上的一个动点，设其横坐标为．

(1)求抛物线的解析式;

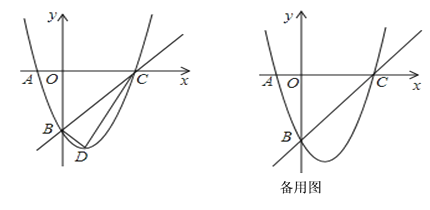
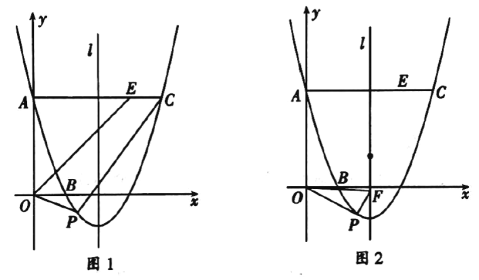
(2)如图1，动点在直线下方的抛物线上，连结，当为何值时，四边形面积最大，并求出其最大值，

(3)如图②，是抛物线的对称轴上的一点，连接，在抛物线轴下方的图像上是否存在点使满足:①；②？若存在，求点的坐标，若不存在，请说明理由．

Answer 1

【答案】（1）y=x2-4x+3；（2），当=时，四边形面积最大，最大值是；（3）或

【解析】

（1）首先根据对称性得出抛物线与轴的另一个交点坐标，然后根据两坐标设抛物线解析式，代入点A的坐标，即可得解；

（2）设P坐标，过点P作PF||轴，将四边形OPCE的面积表示为：，计算即可；

（3）区分为P在对称轴左，右两侧进行讨论，借用，构造一线三角形相似，列出等量关系，计算即可．

（1）如图，设抛物线与轴的另一个交点为D

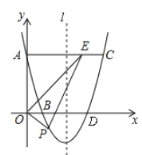
由对称性得：D(3,0)

设抛物线的解析式为：

把A(0,3)代入得：即

∴抛物线的解析式：

（2）如图，过点P作轴，交AC于点F

在中，点A与点C关于对称轴对称

∵A（0,3），∴C（4,3）

∵OE平分，且

∴

∴AE=AO=3

设，则

则，，

故

∵P在BC的下方

∴

∴当时，四边形OPCE的面积最大，最大值为：

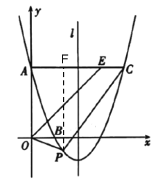
（3）若点P在对称轴左侧，

过点P作交轴于点M，交于点N

由题得：

∴

∵，则，，

∴，解得

此时

若点P在对称轴右侧

过点P作交轴于点N，过点F作交MN于点M

由题得：

∴

∵，则，

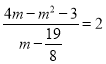∴，解得

此时

综上：点P为，．