题目内容
如果抛物线y=（a-2）x2+3x+a的开口向下，那么a的取值范围是________．
a＜2
分析：根据二次函数的性质可知，当抛物线开口向下时，二次项系数a-2＜0．
解答：因为抛物线y=（a-2）x2+3x+a的开口向下，
所以a-2＜0，即a＜2．
故答案为：a＜2．
点评：本题主要考查了二次函数的性质．用到的知识点：对于二次函数y=ax2+bx+c（a≠0）来说，当a＞0时，抛物线y=ax2+bx+c（a≠0）开口向上；当a＜0时，抛物线y=ax2+bx+c（a≠0）开口向下．
分析：根据二次函数的性质可知，当抛物线开口向下时，二次项系数a-2＜0．
解答：因为抛物线y=（a-2）x2+3x+a的开口向下，
所以a-2＜0，即a＜2．
故答案为：a＜2．
点评：本题主要考查了二次函数的性质．用到的知识点：对于二次函数y=ax2+bx+c（a≠0）来说，当a＞0时，抛物线y=ax2+bx+c（a≠0）开口向上；当a＜0时，抛物线y=ax2+bx+c（a≠0）开口向下．
练习册系列答案
名校课堂系列答案
相关题目
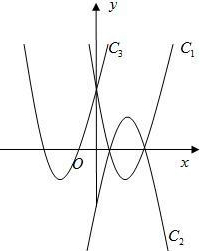如图示：己知抛物线C1，C2关于x轴对称，抛物线C1，C3关于y轴对称．如果抛物线C2的解析式是y=-如果抛物线经过点（2，3），（3，2）和（4，3），则抛物线的顶点是（ ）
| A、（2，3） | B、（3，2） | C、（4，3） | D、无法确定 |