题目内容
 如图,甲船在港口P的北偏西60°方向,距港口80海里的A处,沿AP方向以12海里/时的速度驶向港口P.乙船从港口P出发,沿北偏东15°方向匀速驶离港口P,现两船同时出发,2小时后乙船在甲船的正东方向.求乙船的航行速度.(精确到0.1海里/时,参考数据
如图,甲船在港口P的北偏西60°方向,距港口80海里的A处,沿AP方向以12海里/时的速度驶向港口P.乙船从港口P出发,沿北偏东15°方向匀速驶离港口P,现两船同时出发,2小时后乙船在甲船的正东方向.求乙船的航行速度.(精确到0.1海里/时,参考数据| 2 |
| 3 |
考点:解直角三角形的应用-方向角问题
专题:
分析:作PQ⊥BC于Q,在Rt△PQB中,求出PQ,在Rt△PQC中,求出PQ,据此即可求出乙船的航行速度.
解答:解: 依题意,设乙船速度为x海里/时,2小时后甲船在点B处,乙船在点C处,
依题意,设乙船速度为x海里/时,2小时后甲船在点B处,乙船在点C处,
作PQ⊥BC于Q,
则BP=80-2×12=56海里,PC=2x海里.
在Rt△PQB中,∠BPQ=60°,
∴PQ=BPcos60°=56×
=28.
在Rt△PQC中,∠QPC=45°,
∴PQ=PC•cos45°=
•2x=
x.
x=28,
x=14
.
∴x≈19.7.
答:乙船的航行速度约为19.7海里/时.
 依题意,设乙船速度为x海里/时,2小时后甲船在点B处,乙船在点C处,
依题意,设乙船速度为x海里/时,2小时后甲船在点B处,乙船在点C处,作PQ⊥BC于Q,
则BP=80-2×12=56海里,PC=2x海里.
在Rt△PQB中,∠BPQ=60°,
∴PQ=BPcos60°=56×
| 1 |
| 2 |
在Rt△PQC中,∠QPC=45°,
∴PQ=PC•cos45°=
| ||
| 2 |
| 2 |
| 2 |
x=14
| 2 |
∴x≈19.7.
答:乙船的航行速度约为19.7海里/时.
点评:本难题考查了解直角三角形的应用--方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知点D在点O的北偏西30°方向,点E在点O的北偏东50°方向,那么∠DOE的度数为
如图,已知点D在点O的北偏西30°方向,点E在点O的北偏东50°方向,那么∠DOE的度数为
 现要在三角地ABC内建一中心医院,使医院到A、B两个居民小区的距离相等,并且到公路AB和AC的距离也相等,请确定这个中心医院的位置.
现要在三角地ABC内建一中心医院,使医院到A、B两个居民小区的距离相等,并且到公路AB和AC的距离也相等,请确定这个中心医院的位置. 如图,△ABC是⊙O的内接三角形,AD⊥BC于D点,且sin∠DAC=
如图,△ABC是⊙O的内接三角形,AD⊥BC于D点,且sin∠DAC=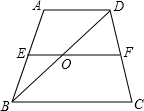 如图,在梯形ABCD中,AD∥BC,中位线EF交BD于点O,若FO-EO=6,则BC-AD为
如图,在梯形ABCD中,AD∥BC,中位线EF交BD于点O,若FO-EO=6,则BC-AD为