题目内容
【题目】（1）（问题情境）
课外兴趣小组活动时，老师提出了如下问题：
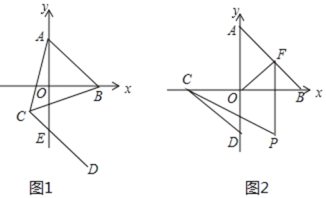
如图①，在△ABC中，AD是△ABC的中线，若AB＝10，AC＝8，求AD的取值范围．
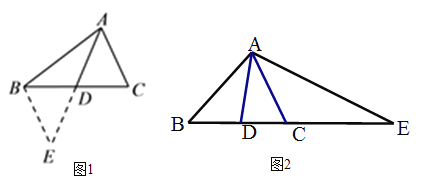
小明在组内经过合作交流，得到了如下的解决方法：延长AD至点E，使DE＝AD，连接BE．请根据小明的方法思考：
Ⅰ.由已知和作图能得到△ADC≌△EDB，依据是________．
A．SSS B．SAS C．AAS D．ASA
Ⅱ.由“三角形的三边关系”可求得AD的取值范围是________．
解后反思：题目中出现“中点”、“中线”等条件，可考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形之中．
（2）（学会运用）
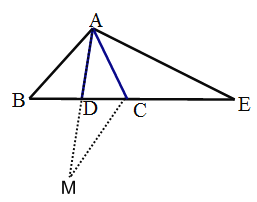
如图②，AD是 △ABC的中线，点E在BC的延长线上，CE=AB, ∠BAC=∠BCA, 求证：AE=2AD.
【答案】（1）Ⅰ.B；Ⅱ. 1＜AD＜9；（2）证明见解析.
【解析】
（1）Ⅰ.根据全等三角形的判定定理解答；
Ⅱ.根据三角形的三边关系定理可得ABBE＜AE＜AB＋BE，结合BE=AC可确定AE的取值范围，易得AD的取值范围；
（2）首先延长AD至M，使DM＝AD，先证明△ABD≌△MCD，进而得出MC＝AB，∠B＝∠MCD，即可得出∠ACM＝∠ACE，再证明△ACM≌△ACE，即可证明结论．
解：（1）Ⅰ.在△ADC和△EDB中，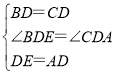
，
∴△ADC≌△EDB（SAS），
故选：B；
Ⅱ.∵△ADC≌△EDB，
∴BE=AC，
∵ABBE＜AE＜AB＋BE，
∴AB AC＜AE＜AB＋AC，即2＜AE＜18，
∴1＜AD＜9，
故答案为：1＜AD＜9；
（2）延长AD至M，使DM＝AD，
∵AD是△ABC的中线，
∴BD＝CD，
在△ABD和△MCD中，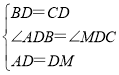
，
∴△ABD≌△MCD（SAS），
∴MC＝AB，∠B＝∠MCD，
∵AB＝CE，
∴CM＝CE，
∵∠BAC＝∠BCA，
∴∠B＋∠BAC＝∠ACB＋∠MCD，即∠ACE＝∠ACM，
在△ACE和△ACM中，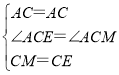
，
∴△ACM≌△ACE（SAS），
∴AE＝AM，
∵AM＝2AD，
∴AE＝2AD．
