题目内容
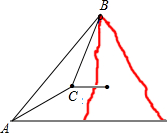 次数学课外活动中,一位同学在山脚下A处测得山顶B的仰角为45°,沿着坡角 30°的斜坡AC走了500米到达C处,又测得山顶B的仰角为60°,求山顶B的高度(
次数学课外活动中,一位同学在山脚下A处测得山顶B的仰角为45°,沿着坡角 30°的斜坡AC走了500米到达C处,又测得山顶B的仰角为60°,求山顶B的高度(| 2 |
| 3 |
考点:解直角三角形的应用-坡度坡角问题
专题:
分析:过点C作CE⊥AD,△ADB是等腰直角三角形,直角△ACE中满足解直角三角形的条件.在直角△BCF中,根据三角函数可得BF,进一步得到BD,即可求出山高.
解答: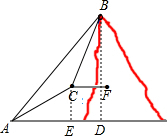 解:过C分别作CE⊥AD与E,CF⊥BD于F.
解:过C分别作CE⊥AD与E,CF⊥BD于F.
∵在Rt△ACE中,AC=1000m,∠CAE=30°,
∴CE=
AC=250m.
∵∠BAD=45°,
∴∠CAB=45°-30°=15°,∠ABD=90°-45°=45°.
∵在Rt△BDF中,∠BDF=60°,
∴∠CBF=90°-60°=30°,
∴∠CBA=45°-30°=15°,
∵∠CAB=15°,
∴∠CBA=∠CAB,
∴BC=AC=500m,
∴在Rt△BCF中,BF=
BC=250
m,
∴山的高度BD为(250
+250)m.
 解:过C分别作CE⊥AD与E,CF⊥BD于F.
解:过C分别作CE⊥AD与E,CF⊥BD于F.∵在Rt△ACE中,AC=1000m,∠CAE=30°,
∴CE=
| 1 |
| 2 |
∵∠BAD=45°,
∴∠CAB=45°-30°=15°,∠ABD=90°-45°=45°.
∵在Rt△BDF中,∠BDF=60°,
∴∠CBF=90°-60°=30°,
∴∠CBA=45°-30°=15°,
∵∠CAB=15°,
∴∠CBA=∠CAB,
∴BC=AC=500m,
∴在Rt△BCF中,BF=
| ||
| 2 |
| 3 |
∴山的高度BD为(250
| 3 |
点评:本题考查了解直角三角形的应用-仰角俯角问题的应用,根据已知得出FC,BF的长是解题关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
下列运算正确的是( )
| A、2m3+m3=3m6 | ||
| B、m3•m2=m6 | ||
| C、(-m4)3=m7 | ||
D、m6÷2m2=
|
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,CD=4,cosA=
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,CD=4,cosA=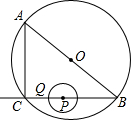 如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.P为BC的中点,动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆,设点Q运动的时间为ts.
如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.P为BC的中点,动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆,设点Q运动的时间为ts.