题目内容
 如图,A为圆O上半圆上的一个三等分点,B是AM的中点,P为直径MN上的一动点,圆O的半径为1,
如图,A为圆O上半圆上的一个三等分点,B是AM的中点,P为直径MN上的一动点,圆O的半径为1,求AP+BP的最小值.
分析:找点A或点B关于MN的对称点,再连接其中一点的对称点和另一点,和MN的交点P就是所求作的位置.根据题意先求出∠CAE,再根据勾股定理求出AE,即可得出PA+PB的最小值.
解答: 解:作点B关于MN的对称点E,连接AE交MN于点P
解:作点B关于MN的对称点E,连接AE交MN于点P
此时PA+PB最小,且等于AE.
作直径AC,连接CE.
根据垂径定理得弧BM=弧ME.
∵A是半圆的三等分点,
∴∠AOM=60°,∠MOE=
∠AOM=30°,
∴∠AOE=90°,
∴∠CAE=45°,
又AC为圆的直径,∴∠AEC=90°,
∴∠C=∠CAE=45°,
∴CE=AE=
AC=
,
即AP+BP的最小值是
.
 解:作点B关于MN的对称点E,连接AE交MN于点P
解:作点B关于MN的对称点E,连接AE交MN于点P此时PA+PB最小,且等于AE.
作直径AC,连接CE.
根据垂径定理得弧BM=弧ME.
∵A是半圆的三等分点,
∴∠AOM=60°,∠MOE=
| 1 |
| 2 |
∴∠AOE=90°,
∴∠CAE=45°,
又AC为圆的直径,∴∠AEC=90°,
∴∠C=∠CAE=45°,
∴CE=AE=
| ||
| 2 |
| 2 |
即AP+BP的最小值是
| 2 |
点评:本题考查了垂径定理及勾股定理的知识,此题的难点是确定点P的位置:找点B关于MN的对称点,再连接其中一点的对称点和另一点,和AE于MN的交点P就是所求作的位置.再根据弧的度数和圆心角的度数求出∠CAE,根据勾股定理求出AE即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
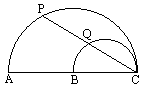
 如图,A为圆O上半圆上的一个三等分点,B是AM的中点,P为直径MN上的一动点,圆O的半径为1,
如图,A为圆O上半圆上的一个三等分点,B是AM的中点,P为直径MN上的一动点,圆O的半径为1,