��Ŀ����
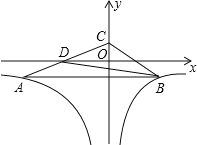
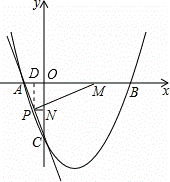
��ͼ��ֱ��y=��3x��3��x�ᡢy��ֱ��ཻ�ڵ�A��C��������C�ҶԳ���Ϊx=1��������y=ax2+bx+c��x���ཻ��A��B���㣮
��1�������A��C�����ꣻ
��2���������ߵĽ���ʽ��
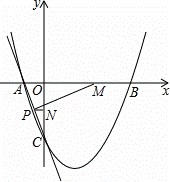
��3������M���߶�AB����ÿ��1����λ���ȵ��ٶ��ɵ�B���A�˶���ͬʱ����N���߶�OC������ͬ���ٶ��ɵ�O���C�˶���������һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶�������PN��x�ᣬ��AC��P�������˶������У��߶�PM�ij����Ƿ������Сֵ�����У��������Сֵ�����ޣ���˵�����ɣ�
�⣺��1����y=��3x��3��
�൱y=0ʱ����3x��3=0�����x=��1��
��A����1��0����
�ߵ�x=0ʱ��y=��3��
��C��0����3����
��2����������y=ax2+bx+c�ĶԳ���Ϊx=1������A����1��0����C��0����3����
��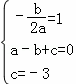 �����
�����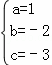 ��
��
�������ߵĽ���ʽΪy=x2��2x��3��
��3���ɶԳ��Եõ�B��3��0�������M�˶���ʱ��Ϊt�루0��t��3������M��3��t��0����N��0����t����P��xP����t����
��PN��OA��
���CPN�ס�CAO��
��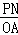 =
= ����
����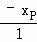 =
=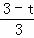 ��
��
��xP=��1��
����P��PD��x���ڵ�D����D����1��0����
��MD=��3��t��������1��=��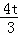 +4��
+4��
��PM2=MD2+PD2=����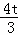 +4��2+����t��2=��25t2��96t+144����
+4��2+����t��2=��25t2��96t+144����
�֡ߩ� =
= ��3��
��3��
�൱t= ʱ��PM2��СֵΪ
ʱ��PM2��СֵΪ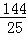 ��
��
�����˶������У��߶�PM�ij��ȴ�����Сֵ ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д���֪x=2��һԪ���η���x2��2mx+4=0��һ���⣬��m��ֵΪ��������
| �� | A�� | 2 | B�� | 0 | C�� | 0��2 | D�� | 0��2 |
ij��ʦ�Ա�������ѧ������ѧ���Գɼ����ɼ�Ϊ����������Ϊ100�֣�����ͳ�Ʒ��������Ƴ�����Ƶ����Ƶ�ʷֲ�����Ƶ���ֲ�ֱ��ͼ���������ͼ���ṩ����Ϣ������������⣺

| ���� | 49.5��59.5 | 59.5��69.5 | 69.5��79.5 | 79.5��89.5 | 89.5��100.5 |
| Ƶ�� | 2 | a | 20 | 16 | 8 |
| Ƶ�� | 0.04 | 0.08 | 0.40 | 0.32 | b |
��1����a��b��ֵ��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3����ʦ���ӳɼ�������80�ֵ�ѧ����ѡ1�˽���ѧϰ���飬��ô��ѡ�е�ѧ����ɼ�������90�ֵĸ����Ƕ��٣�
��ͼ��һ�������������ͼ������ͼ������ͼ��Ϊ�������Σ��丩��ͼΪ�����Σ�������������ǣ�������
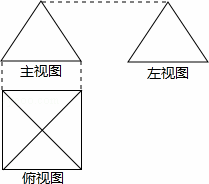
| �� | A�� | ���� | B�� | ������ | C�� | ������ | D�� | ���� |

 ���Ա���x��ȡֵ��ΧΪ��
���Ա���x��ȡֵ��ΧΪ��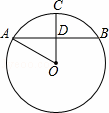
 Oy�У�OΪ����ԭ�㣩����֪������y=x2+bx+c����A��4��0����B��1����3����
Oy�У�OΪ����ԭ�㣩����֪������y=x2+bx+c����A��4��0����B��1����3����