题目内容
菱形ABCD的对角线长为分别AC= ,BD=2,则菱形的内角∠BAD=
,BD=2,则菱形的内角∠BAD=
- A.30°
- B.60°
- C.120°
- D.150°
B
分析:首先根据菱形的性质可得AO= AC,BO=
AC,BO= BD,AC⊥DB,进而得到AO=
BD,AC⊥DB,进而得到AO= ,BO=1,△ABO是直角三角形,再利用勾股定理算出AB的长,证明△ABO是等边三角形,进而算出菱形的内角∠BAD的度数.
,BO=1,△ABO是直角三角形,再利用勾股定理算出AB的长,证明△ABO是等边三角形,进而算出菱形的内角∠BAD的度数.
解答: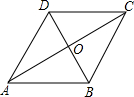 根据题意画出图形:
根据题意画出图形:
∵四边形ABCD是菱形,
∴AO= AC,BO=
AC,BO= BD,AC⊥DB,
BD,AC⊥DB,
∵AC= ,BD=2,
,BD=2,
∴AO= ,BO=1,
,BO=1,
∴AB= =2,
=2,
∴AD=BD=AB=2,
∴△ADB是等边三角形,
∴∠BAD=60°.
故选:B.
点评:此题主要考查了菱形的性质,关键是熟练掌握菱形的性质:①菱形具有平行四边形的一切性质;②菱形的四条边都相等;③菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
分析:首先根据菱形的性质可得AO=
 AC,BO=
AC,BO= BD,AC⊥DB,进而得到AO=
BD,AC⊥DB,进而得到AO= ,BO=1,△ABO是直角三角形,再利用勾股定理算出AB的长,证明△ABO是等边三角形,进而算出菱形的内角∠BAD的度数.
,BO=1,△ABO是直角三角形,再利用勾股定理算出AB的长,证明△ABO是等边三角形,进而算出菱形的内角∠BAD的度数.解答:
 根据题意画出图形:
根据题意画出图形:∵四边形ABCD是菱形,
∴AO=
 AC,BO=
AC,BO= BD,AC⊥DB,
BD,AC⊥DB,∵AC=
 ,BD=2,
,BD=2,∴AO=
 ,BO=1,
,BO=1,∴AB=
 =2,
=2,∴AD=BD=AB=2,
∴△ADB是等边三角形,
∴∠BAD=60°.
故选:B.
点评:此题主要考查了菱形的性质,关键是熟练掌握菱形的性质:①菱形具有平行四边形的一切性质;②菱形的四条边都相等;③菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.

练习册系列答案
相关题目
 如图,菱形ABCD的边长为20cm,∠ABC=120°.动点P、Q同时从点A出发,其中P以4cm/s的速度,沿A→B→C的路线向点C运动;Q以2
如图,菱形ABCD的边长为20cm,∠ABC=120°.动点P、Q同时从点A出发,其中P以4cm/s的速度,沿A→B→C的路线向点C运动;Q以2 如图,菱形ABCD的对角线AC和BD相交于O点,E,F,G,H分别是AB,BC,CD,DA的中点,求证:E,F,G,H四个点在以O为圆心的同一个圆上.
如图,菱形ABCD的对角线AC和BD相交于O点,E,F,G,H分别是AB,BC,CD,DA的中点,求证:E,F,G,H四个点在以O为圆心的同一个圆上. 如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线于点F.
如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线于点F. 如图,菱形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,请说明四边形OCED是矩形.
如图,菱形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,请说明四边形OCED是矩形.