题目内容
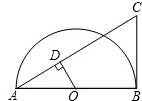如图，AB是半圆O的直径，∠BAC=30°，BC为半圆的切线，且BC=
，则圆心O到AC的距离是________．
3
分析：首先过O作AC的垂线段，再利用三角形相似就可以求出O到AC的距离．
解答：∵BC是⊙O的切线，
∴∠ABC=90°，
∵OD⊥AC，
∴∠ADO=90°，∠A公共，
∴△ABC∽△ADO，
∴
，即OD=
；
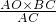在△ABC中，
∠BAC=30°，
∴AC=2BC=8
，
AB=
=12，
∴OA=6=BO，
∴OD=
．
点评：主要利用了相似三角形的对应线段成比例．
分析：首先过O作AC的垂线段，再利用三角形相似就可以求出O到AC的距离．
解答：∵BC是⊙O的切线，
∴∠ABC=90°，
∵OD⊥AC，
∴∠ADO=90°，∠A公共，
∴△ABC∽△ADO，
∴
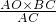，即OD=；在△ABC中，
∠BAC=30°，
∴AC=2BC=8
，AB=
=12，∴OA=6=BO，
∴OD=
．点评：主要利用了相似三角形的对应线段成比例．
练习册系列答案
相关题目
如图，AB是半圆O的直径，AC是弦，点P从点B开始沿BA边向点A以1cm/s的速度移动，若AB长为10cm，点O到AC的距离为4cm．
已知：如图，AB是半圆O的直径，OD是半径，BM切半圆于点B，OC与弦AD平行交BM于点C．
如图，AB是半圆O的直径，点D是半圆上一动点，AB=10，AC=8，当△ACD是等腰三角形时，点D到AB的距离是
如图，AB是半圆O的直径，以OA为直径的半圆O′与弦AC交于点D，O′E∥AC，并交OC于点E，则下列结论：①S△O′OE=
