Question

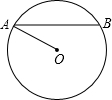
如图所示，已知⊙O的半径为5cm，弦AB的长为8cm，P是AB延长线上一点，BP=2cm，则tan∠OPA等于______．

Answer 1

过C作OC⊥AB于C，
∵OC⊥AB，OC过圆心O，
∴AC=BC=

1

2

AB，
∵AB=8cm，
∴AC=BC=4cm，
∵在Rt△ACO中，∠ACO=90°，AC=4cm，OA=5cm，由勾股定理得：OC=3cm，
∵BP=2cm
∴PC=PB+BC=2cm+4cm=6cm，
在△OCP中，tan∠OPA=

OC

PC

=

3

6

=

1

2

，
故答案为：

1

2

．