题目内容
已知点A(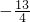 ,y1),B(
,y1),B( ,y2),C(
,y2),C( ,y3)在抛物线y=x2-mx+n(m、n为常数)上,且y2<y1<y3,则m的取值范围是________.
,y3)在抛物线y=x2-mx+n(m、n为常数)上,且y2<y1<y3,则m的取值范围是________.
-9<m<0
分析:首先根据抛物线的开口方向以及图象上点的坐标和y2<y1<y3,得出对称轴的取值范围,进而得出m的取值范围.
解答:∵点A(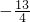 ,y1),B(
,y1),B( ,y2),C(
,y2),C( ,y3)在抛物线y=x2-mx+n(m、n为常数)上,y2<y1<y3,
,y3)在抛物线y=x2-mx+n(m、n为常数)上,y2<y1<y3,
∴B( ,y2),C(
,y2),C( ,y3)在对称轴右侧,点A(
,y3)在对称轴右侧,点A(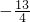 ,y1),在对称轴左侧,
,y1),在对称轴左侧,
且A点到对称轴距离大于B点到对称轴距离,
∴对称轴0>x>(- -
- ),
),
即0>x>- ,
,
∴0> >-
>- ,
,
解得:-9<m<0.
故答案为:-9<m<0.
点评:此题主要考查了二次函数图象上点的特征,根据已知得出对称轴取值范围是解题关键.
分析:首先根据抛物线的开口方向以及图象上点的坐标和y2<y1<y3,得出对称轴的取值范围,进而得出m的取值范围.
解答:∵点A(
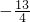 ,y1),B(
,y1),B( ,y2),C(
,y2),C( ,y3)在抛物线y=x2-mx+n(m、n为常数)上,y2<y1<y3,
,y3)在抛物线y=x2-mx+n(m、n为常数)上,y2<y1<y3,∴B(
 ,y2),C(
,y2),C( ,y3)在对称轴右侧,点A(
,y3)在对称轴右侧,点A(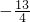 ,y1),在对称轴左侧,
,y1),在对称轴左侧,且A点到对称轴距离大于B点到对称轴距离,
∴对称轴0>x>(-
 -
- ),
),即0>x>-
 ,
,∴0>
 >-
>- ,
,解得:-9<m<0.
故答案为:-9<m<0.
点评:此题主要考查了二次函数图象上点的特征,根据已知得出对称轴取值范围是解题关键.

练习册系列答案
相关题目