题目内容
8.若$\frac{a-b}{b}$=$\frac{2}{3}$,则$\frac{a}{b}$=$\frac{5}{3}$;若$\frac{x}{2}$=$\frac{y}{3}$=$\frac{z}{4}$≠0,则$\frac{2x+5y}{z}$=$\frac{19}{4}$.分析 根据合比性质,可得答案;
根据比例的性质,可用x表示y,用x表示z,根据分式的性质,可得答案.
解答 解:$\frac{a-b}{b}$=$\frac{2}{3}$由合比性质,得
$\frac{a}{b}$=$\frac{2+3}{3}$=$\frac{5}{3}$;
由$\frac{x}{2}$=$\frac{y}{3}$=$\frac{z}{4}$≠0,得
y=$\frac{3x}{2}$,z=2x.
$\frac{2x+5y}{z}$=$\frac{2x+5×\frac{3x}{2}}{2x}$=$\frac{\frac{19}{2}}{2}$=$\frac{19}{4}$,
故答案为:$\frac{5}{3}$,$\frac{19}{4}$.
点评 本题考查了比例的性质,利用了合比性质,比例的性质用x表示y,用x表示z是解题关键.

练习册系列答案
相关题目
18.一个梯形的上底长10cm,中位线长16cm,则其下底长为( )cm.
| A. | 18 | B. | 20 | C. | 22 | D. | 24 |
16.下列式子中结果是负数的是( )
| A. | -|-2| | B. | -(-2) | C. | 2-2 | D. | (-2)2 |
3.-$\frac{1}{5}$的倒数是( )
| A. | -$\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | -5 | D. | 5 |
20.(-3)3的绝对值等于( )
| A. | -9 | B. | 9 | C. | 27 | D. | -27 |
17.据天气预报:2015年元旦某地的最高气温为5℃,最低气温为-1℃,那么这天的最高气温比最低气温高( )
| A. | -6℃ | B. | 4℃ | C. | 6℃ | D. | 5℃ |
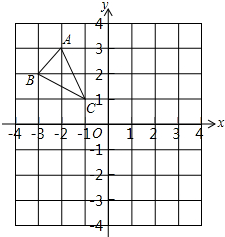 如图,在平面直角坐标系中,将三角形△ABC向下平移5个单位长度,再向右平移3个单位长度,请画出图形△A1B1C1,并写出A1,B1,C1的坐标.
如图,在平面直角坐标系中,将三角形△ABC向下平移5个单位长度,再向右平移3个单位长度,请画出图形△A1B1C1,并写出A1,B1,C1的坐标.