题目内容
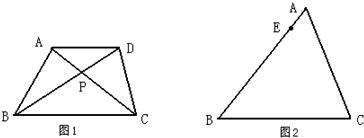
 如图,①在梯形ABCD中,AD∥BC.现有3个关系式:
如图,①在梯形ABCD中,AD∥BC.现有3个关系式:
②AB=AD+BC,③DE=CE,④AE⊥BE.
请在所给的关系式②,③,④中选取两个与①组成条件,剩余的一个作为结论,使得由条件能正确推出结论并说明你的理由.
我选取的条件是关系式________,________和①.(填写序号)
结论是关系式________.(填写序号)
由条件能正确推出结论,理由如下:________.
③ ④ ② 连接AB的中点F与E,
∴EF为梯形ABCD的中位线,
∴EF= (AD+BC)
(AD+BC)
∵AE⊥BE.
∴EF= AB,
AB,
∴AB=AD+BC
分析:首先找到AB的中点F,连接EF得到梯形的中位线,然后利用梯形的中位线定理及直角三角形斜边上的中线等于斜边的一半可以得到结论.
解答: 答:选取的条件是③④和①,
答:选取的条件是③④和①,
结论关系式为:②;
证明:连接AB的中点F与E,
∴EF为梯形ABCD的中位线,
∴EF= (AD+BC)
(AD+BC)
∵AE⊥BE.
∴EF= AB,
AB,
∴AB=AD+BC
故答案为:③④,②,
连接AB的中点F与E,
∴EF为梯形ABCD的中位线,
∴EF= (AD+BC)
(AD+BC)
∵AE⊥BE.
∴EF= AB,
AB,
∴AB=AD+BC.
点评:本题考查了梯形的中位线定理及直角三角形斜边上的中线等于斜边的一半,解题关键是构造梯形的中位线并正确的利用梯形的中位线定理.
∴EF为梯形ABCD的中位线,
∴EF=
 (AD+BC)
(AD+BC)∵AE⊥BE.
∴EF=
 AB,
AB,∴AB=AD+BC
分析:首先找到AB的中点F,连接EF得到梯形的中位线,然后利用梯形的中位线定理及直角三角形斜边上的中线等于斜边的一半可以得到结论.
解答:
 答:选取的条件是③④和①,
答:选取的条件是③④和①,结论关系式为:②;
证明:连接AB的中点F与E,
∴EF为梯形ABCD的中位线,
∴EF=
 (AD+BC)
(AD+BC)∵AE⊥BE.
∴EF=
 AB,
AB,∴AB=AD+BC
故答案为:③④,②,
连接AB的中点F与E,
∴EF为梯形ABCD的中位线,
∴EF=
 (AD+BC)
(AD+BC)∵AE⊥BE.
∴EF=
 AB,
AB,∴AB=AD+BC.
点评:本题考查了梯形的中位线定理及直角三角形斜边上的中线等于斜边的一半,解题关键是构造梯形的中位线并正确的利用梯形的中位线定理.

练习册系列答案
相关题目

 24、如图,已知:AD是△ABC中BC边的中线,则S△ABD=S△ACD,依据是
24、如图,已知:AD是△ABC中BC边的中线,则S△ABD=S△ACD,依据是

