题目内容
用面积方法证明:三角形两边中点连线平行于第三边.分析:如图所示.设E,F分别是AB,AC的中点,可求得△EBC与△FBC的面积相等(均为△ABC面积的一半).由于这两个三角形同底BC,因而这两个三角形的顶点E,F在一条与底边BC平行的直线上,所以EF∥BC.
解答: 证明:如图,设E,F分别是AB,AC的中点,
证明:如图,设E,F分别是AB,AC的中点,
∵CE为△ABC的中线,
∴S△BCE=
S△ABC,
同理S△BCF=
S△ABC,
∴S△BCE=S△BCF,
又△BCE、△BCF同底BC,
∴两个三角形的BC边上的高相等,即点E、F到BC的距离相等,
∴EF∥BC.
 证明:如图,设E,F分别是AB,AC的中点,
证明:如图,设E,F分别是AB,AC的中点,∵CE为△ABC的中线,
∴S△BCE=
| 1 |
| 2 |
同理S△BCF=
| 1 |
| 2 |
∴S△BCE=S△BCF,
又△BCE、△BCF同底BC,
∴两个三角形的BC边上的高相等,即点E、F到BC的距离相等,
∴EF∥BC.
点评:本题考查了三角形的面积的求法及等积变换.关键是利用三角形的中线性质:三角形的中线把三角形分为两个面积相等的三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
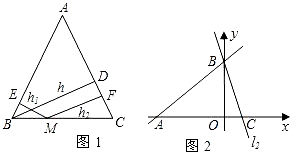

 x+3、l2:y=-3x+3,若l2上的一点M到l1的距离是1,请运用(1)、(2)的结论求出点M的坐标.
x+3、l2:y=-3x+3,若l2上的一点M到l1的距离是1,请运用(1)、(2)的结论求出点M的坐标.
 x+3、l2:y=-3x+3,若l2上的一点M到l1的距离是1,请运用(1)、(2)的结论求出点M的坐标.
x+3、l2:y=-3x+3,若l2上的一点M到l1的距离是1,请运用(1)、(2)的结论求出点M的坐标.