题目内容
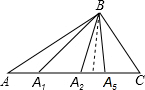
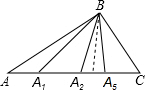在△ABC中，A1、A2、…A5为AC边上不同的点，连接BA1，图中有3个不同的三角形；再连接BA2，图中有6个不同的三角形；如此继续下去，当连接BA5时，则图中不同的三角形共有________个．
21
分析：分别写出连接前几条线段时的三角形的个数，再找出连接第n条线段时三角形的个数，再把n=5代入表达式进行计算即可得解．
解答：连接BA1时，有△AA1B、△ACB、△A1CB共3个，
再连接BA2时，有△AA1B、△AA2B、△ACB、△A1A2B、△A1CB、△A2CB共6个，
…，
依此类推，再连接BAn时，共有三角形个数为：
，
所以，当连接BA5时，不同的三角形共有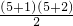
=21．
故答案为：21．
点评：本题是对图形变化规律的考查，比较简单，按照一定的顺序准确找出三角形的个数是解题的关键．
分析：分别写出连接前几条线段时的三角形的个数，再找出连接第n条线段时三角形的个数，再把n=5代入表达式进行计算即可得解．
解答：连接BA1时，有△AA1B、△ACB、△A1CB共3个，
再连接BA2时，有△AA1B、△AA2B、△ACB、△A1A2B、△A1CB、△A2CB共6个，
…，
依此类推，再连接BAn时，共有三角形个数为：
，所以，当连接BA5时，不同的三角形共有
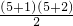=21．故答案为：21．
点评：本题是对图形变化规律的考查，比较简单，按照一定的顺序准确找出三角形的个数是解题的关键．
练习册系列答案
相关题目
如图，在△ABC中，A1，A2，A3是BC边上的四等分点，B1，B2是AC边上的三等分点，AA1与BB1交于C1，B1A2与BB2交于C2，记△AB1C1，△B1B2C2，△B2CA3的面积为S1，S2，S3，则S1：S2：S3=
如图，在△ABC中，A1，B1，C1为三边中点，A2，B2，C2为△A1B1C1三边中点，已知△ABC面积为32厘米2，周长为48厘米，则△A2B2C2面积与周长分别为（ ）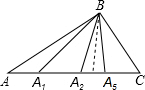
在△ABC中，A1、A2、…A5为AC边上不同的点，连接BA1，图中有3个不同的三角形；再连接BA2，图中有6个不同的三角形；如此继续下去，当连接BA5时，则图中不同的三角形共有
