题目内容
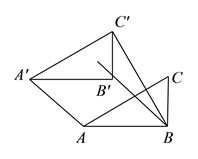
【题目】类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.如图, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,将
,将![]() 沿
沿![]() 的平分线
的平分线![]() 方向平移得到
方向平移得到![]() ,连结
,连结![]() ,
, ![]() .
.
若平移后的四边形![]() 是“等邻边四边形”,求平移的距离(即线段
是“等邻边四边形”,求平移的距离(即线段![]() 的长).
的长).
【答案】![]() 或
或![]() 或
或![]() 或
或![]()
【解析】试题分析:利用“等邻边四边形”的定义和平移的性质(对应线段平行且相等),分四种情况(AA′=AB,AA′=A′C′,A′C′=BC′,BC′=AB)进行讨论计算即可.
试题解析:由![]() ,
, ![]() ,
, ![]() ,得
,得![]() ,
,
∵将![]() 平移得到
平移得到![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(![]() )当
)当![]() 时,
时, ![]() ;
;
(![]() )当
)当![]() 时,
时, ![]() ;
;
(![]() )当
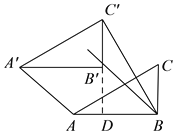
)当![]() 时,如图所示,延长
时,如图所示,延长![]() 交
交![]() 于点
于点![]() ,则
,则![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
设![]() ,则
,则![]() ,
, ![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:
![]() 即
即![]() ,
,
解得: ![]() 或
或![]() (不合题意,舍去),
(不合题意,舍去),
∴![]() ;
;
(![]() )当
)当![]() 时,与(
时,与(![]() )方法同理可得:
)方法同理可得:
![]() 或
或![]() (舍去),
(舍去),
∴![]() ,
,
故平移的距离为![]() 或
或![]() 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目