��Ŀ����
����Ŀ����ͼ������ABCD�ı�BC��x���غ���B��C��Ӧ�ĺ�������һԪ���η���![]() ��������E��AD��y��Ľ��㣬��������Ϊ2����A��C��ֱ�߽�y����F.
��������E��AD��y��Ľ��㣬��������Ϊ2����A��C��ֱ�߽�y����F.
��1����ֱ��AF�Ľ���ʽ��
��2��M��BC��һ�㣬�������Ϊ2�����������ϣ����ܷ��ҵ�һ��P��ʹ![]() �����ܣ������P�����ꣻ�����ܣ���˵������.
�����ܣ������P�����ꣻ�����ܣ���˵������.
��3����Q��x����һ����������AQ,Q���˶�������AQ+![]() �Ƿ������Сֵ�������ڣ������AQ+
�Ƿ������Сֵ�������ڣ������AQ+![]() ��Сֵ��Q�����ꣻ�������ڣ���˵������.
��Сֵ��Q�����ꣻ�������ڣ���˵������.
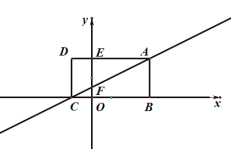
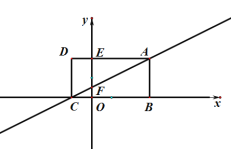
����ͼ
���𰸡���1��![]() ��2����
��2����![]() ������Ϊ
������Ϊ![]() ��
��![]() ��
��![]() ��
��![]() .
.
![]()
![]()
![]()
��������
��1����һԪ���η���![]() �����ɵõ���B,C�����꣬��E������Ϊ2��
�����ɵõ���B,C�����꣬��E������Ϊ2��
���ɵõ���A,C�����꣬�ô���ϵ�����������ֱ��AF�Ľ���ʽ��
��2���ֵ�P��![]() ���
���![]() �������������������.
�������������������.
![]() ����A����
����A����![]() ��ĶԳƵ�
��ĶԳƵ�![]() ����
����![]() ��
��![]() �ڵ�M,��
�ڵ�M,��![]() ���ڵ�Q����
���ڵ�Q����![]() ��Ϊ����.
������.
��1����һԪ���η���![]() ��
��
![]()
���![]()
E��AD��y��Ľ��㣬��������Ϊ2��
![]()
��ֱ��AF�Ľ���ʽΪ![]()
�ѵ�A,C��������룬
![]()
��ã�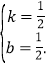
��ֱ��AF�Ľ���ʽΪ![]()
![]() ����P��
����P��![]() ����ʱ�����
����ʱ�����![]()
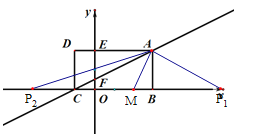
![]()
![]()
��ã�![]() ��
��![]()
��ʱ��![]() ������Ϊ
������Ϊ![]() ��
��![]()
����P��![]() ����������ʱ����
����������ʱ����![]()
![]() =S����ABOP-
=S����ABOP-![]() -
-![]() =7.
=7.
![]()
��ã�![]()
��ʱ��![]() ������Ϊ
������Ϊ![]() .
.
����P��![]() �Ḻ������ʱ����
�Ḻ������ʱ����![]()
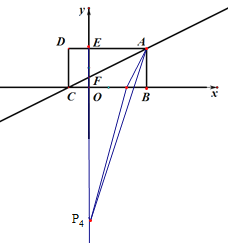
![]()
��ã�![]()
��ʱ��![]() ������Ϊ
������Ϊ![]() .
.
![]() ����A����
����A����![]() ��ĶԳƵ�
��ĶԳƵ�![]() ����
����![]() ��
��![]() �ڵ�M,��
�ڵ�M,��![]() ���ڵ�Q����
���ڵ�Q����![]() ��Ϊ����.
������.
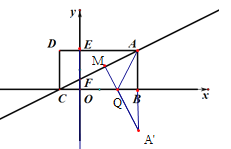
��![]() ����Ϊ
����Ϊ![]()
ֱ��![]() ��ֱ��
��ֱ��![]() ��ֱ��
��ֱ��
ֱ��![]() ��б��
���![]()
ֱ��![]() �ķ���Ϊ��
�ķ���Ϊ�� ![]()
��![]() ʱ��
ʱ��![]()
����![]() ������Ϊ
������Ϊ![]()
��ʱ��![]()
![]()
![]()
AQ+![]() ����СֵΪ
����СֵΪ![]()