题目内容
(1)请阅读材料并填空:问题:如图1,在等边三角形ABC内有一点P,且PA=2,PB=
| 3 |
李明同学的思路是:将△BPC绕点B顺时针旋转60°,画出旋转后的图形(如图2).连接PP′.
根据李明同学的思路,进一步思考后可求得∠BPC=
(2)请你参考李明同学的思路,探究并解决下列问题:如图3,在正方形ABCD内有一点P,且PA=
| 5 |
| 2 |
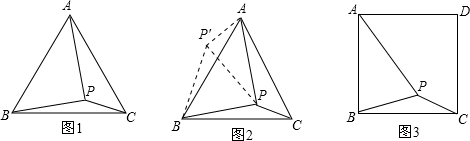
分析:根据旋转得出AP′=CP=1,BP′=BP=
,∠PBC=∠P′BA,∠AP′B=∠BPC,求出∠ABP′+∠ABP=60°,得到等边△BPP′,推出PP′=
,∠BP′P=60°,求出∠AP′P=90°即可求出∠BPC;过点B作BM⊥AP′,交AP′的延长线于点M,由∠MP′B=30°,求出BM=
,P′M=
,根据勾股定理即可求出答案;
(2)求出∠BEP=
(180°-90°)=45°,根据勾股定理的逆定理求出∠AP′P=90°,推出∠BPC=∠AEB=90°+45°=135°;过点B作BF⊥AE,交AE的延长线于点F,求出FE=BF=1,AF=2,关键勾股定理即可求出AB.
| 3 |
| 3 |
| ||
| 2 |
| 3 |
| 2 |
(2)求出∠BEP=
| 1 |
| 2 |
解答:(1)解:∵等边△ABC,
∴∠ABC=60°,
将△BPC绕点B顺时针旋转60°得出△ABP′,
∴AP′=CP=1,BP′=BP=
,∠PBC=∠P′BA,∠AP′B=∠BPC,
∵∠PBC+∠ABP=∠ABC=60°,
∴∠ABP′+∠ABP=∠ABC=60°,
∴△BPP′是等边三角形,
∴PP′=
,∠BP′P=60°,
∵AP′=1,AP=2,
∴AP′2+PP′2=AP2,
∴∠AP′P=90°,
∴∠BPC=∠AP′B=90°+60°=150°,
过点B作BM⊥AP′,交AP′的延长线于点M,
∴∠MP′B=30°,BM=
,
由勾股定理得:P′M=
,
∴AM=1+
=
,
由勾股定理得:AB=
=
,
过答案为:150°,
.
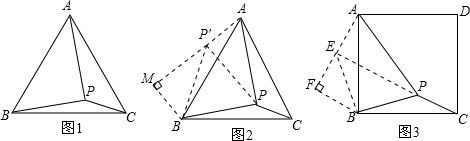
(2)解:将△BPC绕点B逆时针旋转90°得到△AEB,
与(1)类似:可得:AE=PC=1,BE=BP=
,∠BPC=∠AEB,∠ABE=∠PBC,
∴∠EBP=∠EBA+∠ABP=∠ABC=90°,
∴∠BEP=
(180°-90°)=45°,
由勾股定理得:EP=2,
∵AE=1,AP=
,EP=2,
∴AE2+PE2=AP2,
∴∠AEP=90°,
∴∠BPC=∠AEB=90°+45°=135°,
过点B作BF⊥AE,交AE的延长线于点F;
∴∠FEB=45°,
∴FE=BF=1,
∴AF=2;
∴在Rt△ABF中,由勾股定理,得AB=
;
∴∠BPC=135°,正方形边长为
.
答:∠BPC的度数是135°,正方形ABCD的边长是
.
∴∠ABC=60°,
将△BPC绕点B顺时针旋转60°得出△ABP′,
∴AP′=CP=1,BP′=BP=
| 3 |
∵∠PBC+∠ABP=∠ABC=60°,
∴∠ABP′+∠ABP=∠ABC=60°,
∴△BPP′是等边三角形,
∴PP′=
| 3 |
∵AP′=1,AP=2,
∴AP′2+PP′2=AP2,
∴∠AP′P=90°,
∴∠BPC=∠AP′B=90°+60°=150°,
过点B作BM⊥AP′,交AP′的延长线于点M,
∴∠MP′B=30°,BM=
| ||
| 2 |
由勾股定理得:P′M=
| 3 |
| 2 |
∴AM=1+
| 3 |
| 2 |
| 5 |
| 2 |
由勾股定理得:AB=
| AM2+BM2 |
| 7 |
过答案为:150°,
| 7 |

(2)解:将△BPC绕点B逆时针旋转90°得到△AEB,
与(1)类似:可得:AE=PC=1,BE=BP=
| 2 |
∴∠EBP=∠EBA+∠ABP=∠ABC=90°,
∴∠BEP=
| 1 |
| 2 |
由勾股定理得:EP=2,
∵AE=1,AP=
| 5 |
∴AE2+PE2=AP2,
∴∠AEP=90°,
∴∠BPC=∠AEB=90°+45°=135°,
过点B作BF⊥AE,交AE的延长线于点F;
∴∠FEB=45°,
∴FE=BF=1,
∴AF=2;
∴在Rt△ABF中,由勾股定理,得AB=
| 5 |
∴∠BPC=135°,正方形边长为
| 5 |
答:∠BPC的度数是135°,正方形ABCD的边长是
| 5 |
点评:本题主要考查对勾股定理及逆定理,等边三角形的性质和判定,等腰三角形的性质,含30度角的 直角三角形的性质,正方形的性质,旋转的性质等知识点的理解和掌握,正确作辅助线并能根据性质进行证明是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
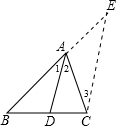 E∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
E∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明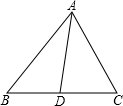 []
[]
 中,∠
中,∠ ,∠
,∠ ,利用此等腰直角三角形你能求出
,利用此等腰直角三角形你能求出 的值吗?
的值吗?
 到点
到点 ,使
,使 ,连结
,连结 .
. (
( ).
). .
. ,
, .
. .
. .
. 的值;
的值; ,∠
,∠ ,
, ;图2中,∠
;图2中,∠ ,∠
,∠ ,
, .图3是小刘所做的一个实验:他将△
.图3是小刘所做的一个实验:他将△ 的直角边
的直角边 与△
与△ 的斜边
的斜边 重合在一起,并将△
重合在一起,并将△ 方向移动.在移动过程中,
方向移动.在移动过程中, 、
、 两点始终在
两点始终在 重合).
重合). 的度数逐渐__________.(填“不变”、“变大”、“变小”)
的度数逐渐__________.(填“不变”、“变大”、“变小”) ?如果存在,求出
?如果存在,求出 的长度;如果不存在,请说明理由.
的长度;如果不存在,请说明理由.
 中,∠
中,∠ ,∠
,∠ ,利用此等腰直角三角形你能求出
,利用此等腰直角三角形你能求出 的值吗?
的值吗?
 到点
到点 ,使
,使 ,连结
,连结 .
. (
( ).
). .
. ,
, .
. .
. .
. 的值;
的值; ,∠
,∠ ,
, ;图2中,∠
;图2中,∠ ,∠
,∠ ,
, .图3是小刘所做的一个实验:他将△
.图3是小刘所做的一个实验:他将△ 的直角边
的直角边 与△
与△ 的斜边
的斜边 重合在一起,并将△
重合在一起,并将△ 方向移动.在移动过程中,
方向移动.在移动过程中, 、
、 两点始终在
两点始终在 重合).
重合). 的度数逐渐__________.(填“不变”、“变大”、“变小”)
的度数逐渐__________.(填“不变”、“变大”、“变小”) ?如果存在,求出
?如果存在,求出 的长度;如果不存在,请说明理由.
的长度;如果不存在,请说明理由.

 ,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.在比例式
,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.在比例式 中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明 就可以转化成证AE=AC.
就可以转化成证AE=AC. ,
,

