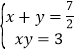ЬтФПФкШн
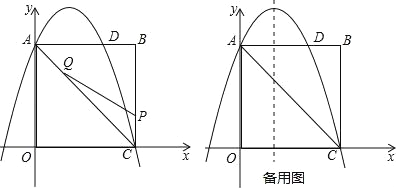
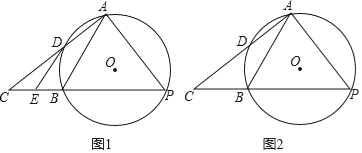
ЁОЬтФПЁПвбжЊABЪЧЁбOЕФЯвЃЌЕуPЪЧгХЛЁABЩЯЕФвЛИіЖЏЕуЃЌСЌНгAPЃЌЙ§ЕуAзїAPЕФДЙЯпЃЌНЛPBЕФбгГЄЯпгкЕуCЃЎ
(1)ШчЭМ1ЃЌACгыЁбOЯрНЛгкЕуDЃЌЙ§ЕуDзїЁбOЕФЧаЯпЃЌНЛPCгкЕуEЃЌШєDEЁЮABЃЌЧѓжЄЃКPA=PBЃЛ
(2)ШчЭМ2ЃЌвбжЊЁбOЕФАыОЖЮЊ2ЃЌAB=2![]() ЃЎ
ЃЎ
ЂйЕБЕуPдкгХЛЁABЩЯдЫЖЏЪБЃЌЁЯCЕФЖШЪ§ЮЊЁЁ ЁЁЁуЃЛ
ЂкЕБЕуPдкгХЛЁABЩЯдЫЖЏЪБЃЌЁїABPЕФУцЛ§ЫцжЎБфЛЏЃЌЧѓЁїABPУцЛ§ЕФзюДѓжЕЃЛ
ЂлЕБЕуPдкгХЛЁABЩЯдЫЖЏЪБЃЌЁїABCЕФУцЛ§ЫцжЎБфЛЏЃЌЁїABCЕФУцЛ§ЕФзюДѓжЕЮЊЁЁ ЁЁЃЎ
ЁОД№АИЁП(1)жЄУїМћНтЮіЃЛ(2)Ђй30ЃЛЂк3![]() ЃЛЂл6+3
ЃЛЂл6+3![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
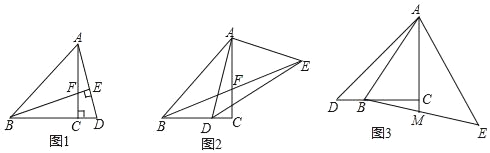
ЃЈ1ЃЉИљОн90ЁуЕФдВжмНЧЫљЖдЕФЯвЪЧжБОЖПЩЕУPDЪЧжБОЖЃЌНсКЯDEЪЧЧаЯпЃЌDEЁЮABЃЌПЩЕУABЁЭPDЃЌРћгУДЙОЖЖЈРэПЩжЄЃЎ
ЃЈ2ЃЉЂйжЛвЊЧѓГіЁЯAOBЕФЖШЪ§ЃЌБуПЩжЊЁЯAPCЕФЖШЪ§ЃЌРћгУЁЯCКЭЁЯAPCЛЅгрЕФЙиЯЕПЩЕУЁЯCЖШЪ§ЃЛЂкЗжЮіКѓПЩвдЗЂЯжЃКPDЁЭABЪБУцЛ§зюДѓЃЛЂлРћгУЁЯCЕФЪ§жЕВЛБфПЩжЊЕуCдкABЮЊЯвЕФЭЌвЛИідВЩЯдЫЖЏЃЌНјЖјевЕНCЕудкКЮДІПЩЪЙЕУЁїABCУцЛ§зюДѓЃЌДгЖјЧѓжЕЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌСЌНгDPНЛABгкЕуFЃЎ
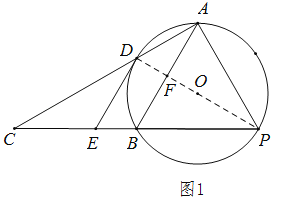
ЁпCAЁЭAPЃЌЁрDPЪЧЁбOЕФжБОЖЃЎ
ЁпDEЪЧЁбOЕФЧаЯпЃЌЁрDEЁЭDPЃЎ
гжЁпDEЁЮABЃЌЁрABЁЭDPЃЌЁрDPДЙжБЦНЗжABЃЈДЙОЖЖЈРэЃЉЃЌЁрPAЃНPBЃЛ
ЃЈ2ЃЉЂйСЌНгOAЁЂOBЃЌгЩЃЈ1ЃЉжЊЃЌDPДЙжБЦНЗжABЃЎ
ЁпABЃН2![]() ЃЌЁрAFЃНBF
ЃЌЁрAFЃНBF![]() ЃЎ
ЃЎ
ЁпЁбOЕФАыОЖЪЧ2ЃЌЁрOAЃНOBЃН2ЃЌЁрsinЁЯAOF![]() ЃЌЁрЁЯAOFЃН60ЁуЃЌЁрЁЯAOBЃН120ЁуЃЌЁрЁЯAPB
ЃЌЁрЁЯAOFЃН60ЁуЃЌЁрЁЯAOBЃН120ЁуЃЌЁрЁЯAPB![]() ЁЯAOBЃН60ЁуЃЎ
ЁЯAOBЃН60ЁуЃЎ
ЁпCAЁЭAPЃЌЁрЁЯC+ЁЯAPBЃН90ЁуЃЌЁрЁЯCЃН30ЁуЃЛ
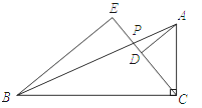
ЂкЕБЕуPдкгХЛЁABЩЯдЫЖЏЪБЃЌЁїABPЕФУцЛ§гЩЕуPЕНABЕФОрРыОіЖЈЃЎ

ИљОнЭМаЮЕФаджЪПЩжЊЃКШчЭМ2ЃЌЕБЕуPдЫЖЏЕНPDЁЭABЪБЃЌPFМДЪЧзюДѓОрРыЃЎ
ЁпOAЃН2ЃЌPDЁЭABЃЌЁЯAOFЃН60ЁуЃЌЁрOFЃН1ЃЌЁрPFЃНOF+OPЃН1+2ЃН3ЃЌЁрЁїABPЕФУцЛ§зюДѓжЕЪЧЃК![]() ABPF
ABPF![]() 3ЃН3
3ЃН3![]() ЃЛ
ЃЛ
ЂлгЩЂйжЊдкБфЛЏЙ§ГЬжаЁЯACBЃН30ЁуКуГЩСЂЃЌЁрЕуCдквдABЮЊЯвЕФФГИідВЩЯдЫЖЏЃЌЩшетИідВЕФдВаФЮЊHЃЌШчЭМ3ЫљЪОЃЎ
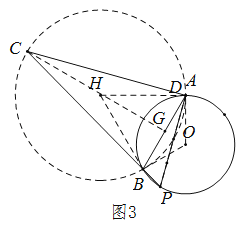
СЌНгAHЁЂBHЃЌЁрЁЯAHBЃН2ЁЯACBЃН60ЁуЃЎ
ЁпAHЃНBHЃЌЁрЁїABHЪЧЕШБпШ§НЧаЮЃЎ
ЁпABЃН2![]() ЃЌЁрЁбHЕФАыОЖHAЃН2
ЃЌЁрЁбHЕФАыОЖHAЃН2![]() ЃЌзїCGЁЭABЃЌЯдШЛЃЌЕБCЕудЫЖЏЕНCGОЙ§дВаФHЪБЁїABCУцЛ§зюДѓЃЎ
ЃЌзїCGЁЭABЃЌЯдШЛЃЌЕБCЕудЫЖЏЕНCGОЙ§дВаФHЪБЁїABCУцЛ§зюДѓЃЎ
ДЫЪБЃЌCGЃНCH+HGЃЌCHЃН2![]() ЃЎ
ЃЎ
ЁпHGЁЭABЃЌABЃН2![]() ЃЌЁрHGЃНAHsin60ЁуЃН3ЃЌЁрCGЃН2
ЃЌЁрHGЃНAHsin60ЁуЃН3ЃЌЁрCGЃН2![]() 3ЃЌЁрЁїABCУцЛ§зюДѓжЕЪЧЃК
3ЃЌЁрЁїABCУцЛ§зюДѓжЕЪЧЃК
![]() ABCG
ABCG![]() ЃЈ2
ЃЈ2![]() 3ЃЉЃН6+3
3ЃЉЃН6+3![]() ЃЎ
ЃЎ

 ЦкФЉН№ХЦОэЯЕСаД№АИ
ЦкФЉН№ХЦОэЯЕСаД№АИ ЧсЫЩПЮЬУБъзМСЗЯЕСаД№АИ
ЧсЫЩПЮЬУБъзМСЗЯЕСаД№АИ