Question

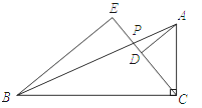
【题目】已知：如图，Rt△ABC中，∠ACB=90°，P是边AB上一点，AD⊥CP，BE⊥CP，垂足分别为D、E，已知AB=3，BC=3，BE=5．求DE的长．

Answer 1

【答案】

【解析】

在Rt△ABC中，由勾股定理求得AC的长，在Rt△BCE中，由勾股定理求得CE的长，由AD⊥CP，得∠DAC+∠ACD=90°，又∠ACD+∠BCE=90°，根据同角的余角相等可得∠DAC=∠BCE，再结合∠BEC=∠ADC=90°，易证△ACD∽△CBE，于是=，易求CD，进而可求DE．

解：∵∠ACB=90°，AB=，BC=，

∴AC=3，

同理可求CE=，

∵AD⊥CP，

∴∠DAC+∠ACD=90°，

∵∠ACD+∠BCE=90°，

∴∠DAC=∠BCE，

又∵∠BEC=∠ADC=90°，

∴△ACD∽△CBE，

∴=，

∴=，

∴CD=，

∴DE=﹣=．