Question

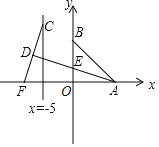
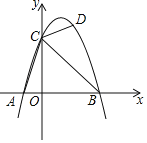
【题目】如图，已知二次函数y＝﹣x2+2x+3的图象与x轴相交于点A，B，与y轴相交于点C，连接AC，BC．该函数在第一象限内的图象上是否存在一点D，使得CB平分∠ACD？若存在，求点D的坐标，若不存在，说明理由．

Answer 1

【答案】存在， .

【解析】

过点C作CE⊥y轴，交抛物线于点E，过点D作DH⊥CE于H，证明∠1＝∠2，由tan∠2＝tan∠1得 的值，进而设D（m，﹣m2+2m+3），列出m的方程求得m便可．

存在．理由如下：

如图，过点C作CE⊥y轴，交抛物线于点E，过点D作DH⊥CE于H，

当x＝0时，y＝3，则C（0，3），

当y＝0时，﹣x2+2x+3＝0，

∴x＝﹣1或3，则A（﹣1，0），B（3，0），

∴OB＝OC＝3，

∴∠OCB＝∠OBC＝∠ECB＝45°，

∵∠ACB＝∠DCB，

∴∠1＝∠2，

所以tan∠2＝tan∠1＝ ，

即

设D（m，﹣m2+2m+3），

则 ，

解得m1＝0（舍去），m2＝ ，

所以D（ ）．