题目内容
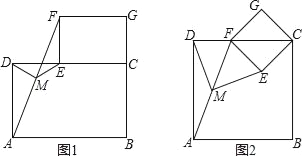
【题目】如图,已知![]() 两点的坐标分别为
两点的坐标分别为![]() ,点
,点![]() 分别是直线
分别是直线![]() 和x轴上的动点,
和x轴上的动点,![]() ,点
,点![]() 是线段
是线段![]() 的中点,连接
的中点,连接![]() 交
交![]() 轴于点
轴于点![]() ;当⊿
;当⊿![]() 面积取得最小值时,
面积取得最小值时,![]() 的值是( )
的值是( )
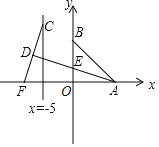
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
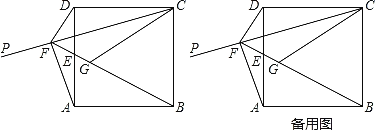
如图,设直线x=-5交x轴于K.由题意KD=![]() CF=5,推出点D的运动轨迹是以K为圆心,5为半径的圆,推出当直线AD与⊙K相切时,△ABE的面积最小,作EH⊥AB于H.求出EH,AH即可解决问题.
CF=5,推出点D的运动轨迹是以K为圆心,5为半径的圆,推出当直线AD与⊙K相切时,△ABE的面积最小,作EH⊥AB于H.求出EH,AH即可解决问题.
如图,设直线x=-5交x轴于K.由题意KD=![]() CF=5,
CF=5,
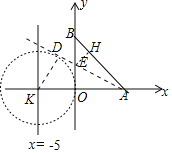
∴点D的运动轨迹是以K为圆心,5为半径的圆,
∴当直线AD与⊙K相切时,△ABE的面积最小,
∵AD是切线,点D是切点,
∴AD⊥KD,
∵AK=13,DK=5,
∴AD=12,
∵tan∠EAO=![]() ,
,
∴![]() ,
,
∴OE=![]() ,
,
∴AE=![]() ,
,
作EH⊥AB于H.
∵S△ABE=![]() ABEH=S△AOB-S△AOE,
ABEH=S△AOB-S△AOE,
∴EH=![]() ,
,
∴![]() ,
,
∴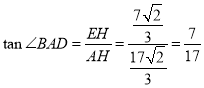 ,
,
故选B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目