题目内容
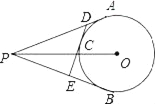
【题目】如图，PA、PB切⊙O于A、B，点C在弧AB上，DE切⊙O于C，交PA、PB于D、E，已知PO=13cm，⊙O的半径为5cm，则△PDE的周长是_____．
【答案】24cm
【解析】
连接OA、OB，由切线长定理可得：PA=PB，DA=DC，EC=EB；由勾股定理可得PA的长，△PDE的周长=PD+DC+CE+PE=PD+DA+PE+EB=PA+PB，即可求得△PDE的周长.
解：连接OA、OB，如图所示：
∵PA、PB为圆的两条切线，
∴由切线长定理可得：PA=PB，
同理可知：DA=DC，EC=EB；
∵OA⊥PA，OA=5，PO=13，
∴由勾股定理得：PA=12，
∴PA=PB=12；
∵△PDE的周长=PD+DC+CE+PE，DA=DC，EC=EB；
∴△PDE的周长=PD+DA+PE+EB=PA+PB=24，
故此题应该填24cm.
练习册系列答案
相关题目
