题目内容
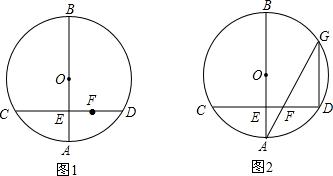
11.如图1,AB为⊙O的直径,弦CD⊥AB于点E,点F在线段ED上.连接AF并延长交⊙O于点G,在CD的延长线上取一点P,使PF=PG.(1)依题意补全图形,判断PG与⊙O的位置关系,并证明你的结论;
(2)如图2,当E为半径OA的中点,DG∥AB,且$OA=2\sqrt{3}$时,求PG的长.
分析 (1)先补全图形,如图1,连接OG,根据等腰三角形的性质,由PF=PG,∠1=∠2.由OG=OA得到∠3=∠A,而∠A+∠AFE=90°,加上∠2=∠AFE,所以∠3+∠1=90°,于是可根据切线的性质判断PG与⊙O相切;
(2)如图2,连接CG,利用DG∥AB得到∠GDC=∠OEC=90°,则根据圆周角定理得CG为⊙O的直径,由于OE=$\frac{1}{2}$OA=$\frac{1}{2}$OC,根据含30度的直角三角形三边的关系得∠C=30°,然后在Rt△CGP,利用三角函数可计算出PG的长.
解答 解:(1)如图1,PG与⊙O相切.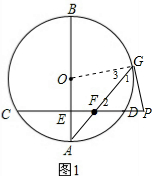
证明如下:连接OG,
∵PF=PG,
∴∠1=∠2.
又∵OG=OA,
∴∠3=∠A,
∵CD⊥AB于点E,
∴∠A+∠AFE=90°,
又∵∠2=∠AFE,
∴∠3+∠1=90°,即∠OGP=90°,
∴OG⊥PG.
∵OG为⊙O的半径,
∴PG与⊙O相切;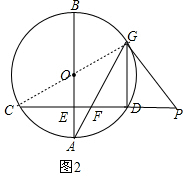
(2)解:如图2,连接CG,
∵CD⊥AB于点E,
∴∠OEC=90°,
∵DG∥AB,
∴∠GDC=∠OEC=90°,
∴CG为⊙O的直径.
∵E为半径OA的中点,
∴OE=$\frac{1}{2}$OA=$\frac{1}{2}$OC,
∴∠C=30°,
而PG与⊙O相切,
∵∠CGP=90°,
∴PG=CG•tan30°=4$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=4.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了解直角三角形.

练习册系列答案
相关题目
2. 如图:点A、B、C、D为⊙O上的四等分点,动点P从圆心O出发,沿O-C-D-O的路线做匀速运动.设运动的时间为t秒,∠APB的度数为y.则下列图象中表示y与t之间函数关系最恰当的是( )
如图:点A、B、C、D为⊙O上的四等分点,动点P从圆心O出发,沿O-C-D-O的路线做匀速运动.设运动的时间为t秒,∠APB的度数为y.则下列图象中表示y与t之间函数关系最恰当的是( )
 如图:点A、B、C、D为⊙O上的四等分点,动点P从圆心O出发,沿O-C-D-O的路线做匀速运动.设运动的时间为t秒,∠APB的度数为y.则下列图象中表示y与t之间函数关系最恰当的是( )
如图:点A、B、C、D为⊙O上的四等分点,动点P从圆心O出发,沿O-C-D-O的路线做匀速运动.设运动的时间为t秒,∠APB的度数为y.则下列图象中表示y与t之间函数关系最恰当的是( )| A. | 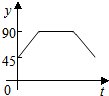 | B. | 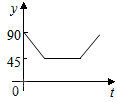 | C. | 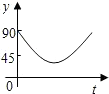 | D. | 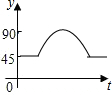 |
1.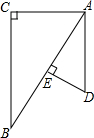 如图,已知△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列一个条件后,仍无法判定△ABC∽△DAE的是( )
如图,已知△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列一个条件后,仍无法判定△ABC∽△DAE的是( )
 如图,已知△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列一个条件后,仍无法判定△ABC∽△DAE的是( )
如图,已知△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列一个条件后,仍无法判定△ABC∽△DAE的是( )| A. | $\frac{AC}{DE}$=$\frac{AB}{AD}$ | B. | ∠B=∠D | C. | AD∥BC | D. | ∠BAC=∠D |
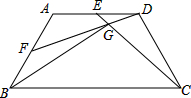 如图,已知:在梯形ABCD中,AD∥BC,∠A=120°,AB=AD=CD,点E、点F分别为线段AD、AB的中点,连接CE、DF,CE与DF相交于点G,连接BG.若DG=2,则线段BG的长为2$\sqrt{13}$.
如图,已知:在梯形ABCD中,AD∥BC,∠A=120°,AB=AD=CD,点E、点F分别为线段AD、AB的中点,连接CE、DF,CE与DF相交于点G,连接BG.若DG=2,则线段BG的长为2$\sqrt{13}$.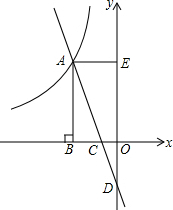 如图,直线y=kx-2与双曲线y=-$\frac{6}{x}$(x<0)交于点A,与x轴交于点C,与y轴交于点D.AB⊥x轴于点B,AE⊥y轴于点E,△ABC的面积为2.
如图,直线y=kx-2与双曲线y=-$\frac{6}{x}$(x<0)交于点A,与x轴交于点C,与y轴交于点D.AB⊥x轴于点B,AE⊥y轴于点E,△ABC的面积为2.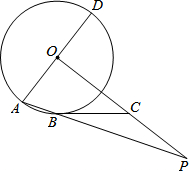 如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P.点C在OP上,且BC=PC.
如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P.点C在OP上,且BC=PC.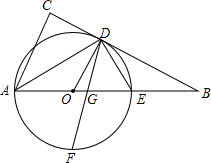 如图,E是△ABC的边AB上一点,以AE为直径的⊙O经过BC上的一点D,且OD∥AC,∠ADE的平分线DF交AB于G,交⊙O于F,且BD=BG
如图,E是△ABC的边AB上一点,以AE为直径的⊙O经过BC上的一点D,且OD∥AC,∠ADE的平分线DF交AB于G,交⊙O于F,且BD=BG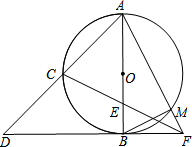 如图,AB是⊙O的直径,C是$\widehat{AB}$的中点,延长AC至点D,使AC=CD,DB的延长线交CE的延长线于点F,AF交⊙O于点M,连接BM.
如图,AB是⊙O的直径,C是$\widehat{AB}$的中点,延长AC至点D,使AC=CD,DB的延长线交CE的延长线于点F,AF交⊙O于点M,连接BM.