题目内容
9. 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,客车行驶时间为x(h),设客车离甲地的距离为y1(km),其中:y1=60x(0≤x≤10);出租车离甲地的距离为y2(km),y1,y2与x的函数关系图象如图所示:
一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,客车行驶时间为x(h),设客车离甲地的距离为y1(km),其中:y1=60x(0≤x≤10);出租车离甲地的距离为y2(km),y1,y2与x的函数关系图象如图所示:(1)根据图象,求出y2关于x的函数关系式;
(2)两车何时相遇?相遇时出租车离甲地的距离是多少千米?
(2)甲、乙两地间有P、Q两个加油站,相距200km,若客车进入P站加油时,出租车恰好进入Q站加油.求P加油站到甲地的距离.
分析 (1)根据待定系数法即可求出一次函数解析式;
(2)解方程组即可得出结果;
(3)分两种情况:①P加油站在甲地与Q加油站之间时;②Q加油站在甲地与P加油站之间时;根据关系列出方程,解方程即可.
解答 解:(1)设y2的解析式为:y2=kx+b,∵函数图象经过点(0,600),(6,0),
则$\left\{\begin{array}{l}{b=600}\\{6k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-100}\\{b=600}\end{array}\right.$,
∴y2=-100x+600(0≤x≤6);
(2)由图可知,点M即为两车相遇点,由$\left\{\begin{array}{l}{y=60x}\\{y=-100x+600}\end{array}\right.$,
解得:x=$\frac{15}{4}$,
再代入y2=-100x+600(0≤x≤6)得:y2=225,
∴相遇时出租车离甲地的距离是225千米.
(3)设两车距离为S,
①P加油站在甲地与Q加油站之间时,(-100x+600)-60x=200,
解得x=$\frac{5}{2}$,
此时,A加油站距离甲地:60×$\frac{5}{2}$=150km,
②Q加油站在甲地与P加油站之间时,60x-(-100x+600)=200,
解得x=5,
此时,A加油站距离甲地::60×5=300km,
综上所述,A加油站到甲地距离为150km或300km
点评 本题考查了一次函数的应用、二元一次方程组的解法、一次函数解析式的求法;主要根据待定系数法求一次函数解析式,根据图象准确获取信息是解题的关键,(2)注意要分情况讨论.

练习册系列答案
相关题目
16.下列说法中正确的是( )
| A. | 四边相等的四边形是菱形 | |
| B. | 一组对边相等,另一组对边平行的四边形是菱形 | |
| C. | 对角线互相垂直的四边形是菱形 | |
| D. | 对角线互相平分的四边形是菱形 |
 ,则点C对应的实数是___________.
,则点C对应的实数是___________.
 ,那么a的值是( )
,那么a的值是( ) B. 3 C.
B. 3 C.  D.
D. 
 某店因为经营不善欠下38400元的无息贷款的债务,想转行经营服装专卖店又缺少资金.“中国梦想秀”栏目组决定借给该店30000元资金,并约定利用经营的利润偿还债务(所有债务均不计利息).已知该店代理的品牌服装的进价为每件40元,该品牌服装日销售量y(件)与销售价x(元/件)之间的关系可用图中的一条折线(实线)来表示.该店应支付员工的工资为每人每天82元,每天还应支付其它费用为106元(不包含债务).
某店因为经营不善欠下38400元的无息贷款的债务,想转行经营服装专卖店又缺少资金.“中国梦想秀”栏目组决定借给该店30000元资金,并约定利用经营的利润偿还债务(所有债务均不计利息).已知该店代理的品牌服装的进价为每件40元,该品牌服装日销售量y(件)与销售价x(元/件)之间的关系可用图中的一条折线(实线)来表示.该店应支付员工的工资为每人每天82元,每天还应支付其它费用为106元(不包含债务). 如图,在6×6的正方形网格中,△ABC的顶点在格点上,请仅用无刻度的直尺分别在图①、图②中画出△ABC的AB边上的高.
如图,在6×6的正方形网格中,△ABC的顶点在格点上,请仅用无刻度的直尺分别在图①、图②中画出△ABC的AB边上的高.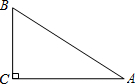 如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=1,
如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=1,