Question

【题目】已知A（a，0），B（0，b），且a、b满足.

（1）填空：a= ，b= ；

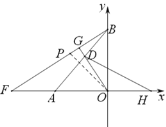
（2）如图1，将ΔAOB沿x轴翻折得ΔAOC，D为线段AB上一动点，OE⊥OD交AC于点E，求S四边形ODAE。

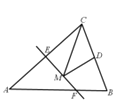
（3）如图2，D为AB上一点，过点B作BF⊥OD于点G，交x轴于点F，点H为x轴正半轴上一点，∠BFO=∠DHO，求证：AF=OH.

Answer 1

【答案】(1)a=-3,b=3;(2)4.5;(3)见解析.

【解析】

（1）根据二次根式的性质及绝对值的非负性可得：a+3=0，a+b=0，求出a、b即可；

（2）根据条件先证明△BOD≌△AOE，然后将四边形ODAE的面积转化为△AOB的面积进行计算即可；

（3）过点O作OP平分∠AOB交BF于P，先证明△BOP≌△OAD，推出OP=AD，再证明△PFO≌△DHA，利用全等的性质即可得出结论.

解：（1）∵a、b满足，

∴a+3=0，a+b=0，

∴a=－3，b=3；

（2）∵由（1）知：A（－3，0），B（0，3）

∴OA=OB=3

∵△AOB沿x轴翻折得△AOC

∴OA=OB=OC，∠AOB＝∠AOC=90°

∴∠ABO＝∠BAO=∠CAO=45°

又∵OE⊥OD，且∠BOD+∠AOD =∠AOB=90°

∴∠AOE+∠AOD=∠BOD+∠AOD=90°

∴∠AOE=∠BOD

∵∠DBO＝∠EAO，OB＝OA,∠BOD＝∠AOE

∴△BOD≌△AOE（ASA）

∴S△AOE=S△BOD

∴S四边形ODAE＝S△AOE + S△AOD = S△BOD + S△AOD =S△AOB＝；

（3）过点O作OP平分∠AOB交BF于P，

∵OP平分∠AOB且OA=OB

∴∠AOP=∠BOP=45°

∴∠AOP=∠BOP=∠OAD

∵BG⊥OD

∴∠OBP+∠BOG=90°

又∵∠AOD+∠BOG=90°

∴∠OBP=∠AOD

∵OB＝OA

∴△BOP≌△OAD（ASA）

∴OP=AD

又∵∠PFO=∠DHO，∠FOP=∠HAD=45°

∴△PFO≌△DHA（AAS）

∴OF＝AH

∴OF－OA=AH－OA，即AF＝OH.