��Ŀ����
��ͼ������OABC�ı�OA,OC�ֱ���x���y���ϣ��ҵ�A������Ϊ
(4��0)����C ������Ϊ��0,2������P���߶�CB�ϣ����� ��3����λ����һֱ
��3����λ����һֱ
��y��kx��b(k��0) ������P���ҰѾ���OABC�ֳ������֡�

С��1:��ֱ���־��� ����һ��D���ҰѾ���OABC�ֳɵ������������ȣ�
����һ��D���ҰѾ���OABC�ֳɵ������������ȣ�
��k ��b��ֵ
С��2:��ֱ���־������α���һ��Q���ҰѾ���OABC�ֳɵ������ֵ������
Ϊ3��29�����Q���ꡣ
(4��0)����C ������Ϊ��0,2������P���߶�CB�ϣ�����
 ��3����λ����һֱ
��3����λ����һֱ��y��kx��b(k��0) ������P���ҰѾ���OABC�ֳ������֡�

С��1:��ֱ���־���
 ����һ��D���ҰѾ���OABC�ֳɵ������������ȣ�
����һ��D���ҰѾ���OABC�ֳɵ������������ȣ���k ��b��ֵ
С��2:��ֱ���־������α���һ��Q���ҰѾ���OABC�ֳɵ������ֵ������
Ϊ3��29�����Q���ꡣ
��1:

��2:Q2��0��
 ��
�� ��1����D��x��0��,������ã�
S����4��2��8,P��3,2��
S��COAP�� ��8��4
��8��4
S��COAP�� ��x+3����2=4
��x+3����2=4
x=1
��D(1,0)
 ���
���
��2��S��PQ1B��

��Q1��4,y��
S��PQ1B�� ��1��(2-y1)=
��1��(2-y1)=
y1��
��Q1��4�� ��
��
��Q2��0��y2��
S��CQ2P�� ��3��(2-y2)=
��3��(2-y2)=
y2��
��Q2��0�� ��
��
S����4��2��8,P��3,2��
S��COAP��
 ��8��4
��8��4 S��COAP��
 ��x+3����2=4
��x+3����2=4x=1
��D(1,0)
 ���
���
��2��S��PQ1B��


��Q1��4,y��
S��PQ1B��
 ��1��(2-y1)=
��1��(2-y1)=
y1��

��Q1��4��
 ��
�� ��Q2��0��y2��
S��CQ2P��
 ��3��(2-y2)=
��3��(2-y2)=
y2��

��Q2��0��
 ��
��
��ϰ��ϵ�д�
 Сѧ�̲���ȫ���ϵ�д�
Сѧ�̲���ȫ���ϵ�д�
�����Ŀ

 ��ͼ��ֱ�x�ᡢy����A��B��PΪAB��һ����PCΪ��AOB����λ�ߣ�PC���ӳ��߽�����������
��ͼ��ֱ�x�ᡢy����A��B��PΪAB��һ����PCΪ��AOB����λ�ߣ�PC���ӳ��߽����������� ��ͼ����Q��
��ͼ����Q�� ����Q�������Ϊ_____________
����Q�������Ϊ_____________

 ��C��Ʊ����Ϊ
��C��Ʊ����Ϊ ��
�� Ԫ�����
Ԫ����� (��)������ʱ��
(��)������ʱ�� ��ʱ��֮���ϵ��ͼ����ͼ��ʾ������˵������ȷ����
��ʱ��֮���ϵ��ͼ����ͼ��ʾ������˵������ȷ���� 
 ��������ʱ��
��������ʱ�� ��
��
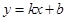 (k��0)��
(k��0)��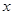 ���ϣ���֪��B1(1��1)��B2(3��2)�� ��Bn��������___________��
���ϣ���֪��B1(1��1)��B2(3��2)�� ��Bn��������___________��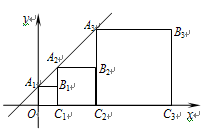
 ,���Ա�����ȡֵ��ΧΪ�� ��
,���Ա�����ȡֵ��ΧΪ�� ��