题目内容
 如图所示,AB=CD,DE⊥AC,BF⊥AC,E、F为垂足,DE=BF.求证:AE=CF.
如图所示,AB=CD,DE⊥AC,BF⊥AC,E、F为垂足,DE=BF.求证:AE=CF.
证明:如图,∵DE⊥AC,BF⊥AC,
∴∠DCE=∠BFA=90°,
∴在Rt△CDE与Rt△ABF中,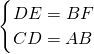 ,
,
∴Rt△CDE≌Rt△ABF(HL),
∴CE=AF,
∴CE-EF=AF-EF,即AE=CF.
分析:通过全等三角形的判定定理HL证得Rt△CDE≌Rt△ABF,则对应边相等:CE=AF,所以根据图示已知得结论.
点评:本题考查了全等三角形的判定与性质.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.
∴∠DCE=∠BFA=90°,
∴在Rt△CDE与Rt△ABF中,
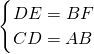 ,
,∴Rt△CDE≌Rt△ABF(HL),
∴CE=AF,
∴CE-EF=AF-EF,即AE=CF.
分析:通过全等三角形的判定定理HL证得Rt△CDE≌Rt△ABF,则对应边相等:CE=AF,所以根据图示已知得结论.
点评:本题考查了全等三角形的判定与性质.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
相关题目
 5、如图所示,AB∥CD,则∠1+∠2+∠3=( )
5、如图所示,AB∥CD,则∠1+∠2+∠3=( )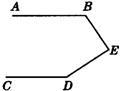 24、已知:如图所示,AB∥CD,若∠ABE=130°,∠CDE=152°,则∠BED=
24、已知:如图所示,AB∥CD,若∠ABE=130°,∠CDE=152°,则∠BED=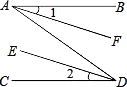 如图所示,AB∥CD,需增加什么条件才能使∠1=∠2成立?
如图所示,AB∥CD,需增加什么条件才能使∠1=∠2成立?
 如图所示,AB∥CD,EG⊥AB,垂足为G,若∠1=42°,则∠E=
如图所示,AB∥CD,EG⊥AB,垂足为G,若∠1=42°,则∠E=