题目内容
已知a=3,且 +(4-b)2=0,则以a、b、c为边组成的三角形面积是
+(4-b)2=0,则以a、b、c为边组成的三角形面积是
- A.6
- B.7
- C.8
- D.9
A
分析:先根据非负数的性质求出b、c的值,再根据勾股定理的逆定理判断出三角形的形状,再由三角形的面积公式解答即可.
解答:∵ +(4-b)2=0,
+(4-b)2=0,
∴ ,解得
,解得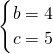 ,
,
∵32+42=52,即a2+b2=c2,
∴以a、b、c为边组成的三角形是直角三角形,
∴S= ab=
ab= ×3×4=6.
×3×4=6.
故选A.
点评:本题考查的是勾股定理的逆定理、非负数的性质及三角形的面积公式,根据勾股定理的逆定理判断出三角形的形状是解答此题的关键.
分析:先根据非负数的性质求出b、c的值,再根据勾股定理的逆定理判断出三角形的形状,再由三角形的面积公式解答即可.
解答:∵
 +(4-b)2=0,
+(4-b)2=0,∴
 ,解得
,解得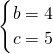 ,
,∵32+42=52,即a2+b2=c2,
∴以a、b、c为边组成的三角形是直角三角形,
∴S=
 ab=
ab= ×3×4=6.
×3×4=6.故选A.
点评:本题考查的是勾股定理的逆定理、非负数的性质及三角形的面积公式,根据勾股定理的逆定理判断出三角形的形状是解答此题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目

 (2012•雅安)已知l1∥l2,且∠1=120°,则∠2=( )
(2012•雅安)已知l1∥l2,且∠1=120°,则∠2=( )