题目内容
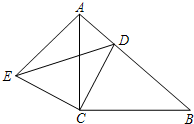
如图，△ABC≌△ADE，B点的对应顶点是D点，若∠BAD=100°，∠CAE=40°，求∠BAC的度数．
∵△ABC≌△ADE，
∴∠BAC=∠DAE，
∴∠BAC-∠CAE=∠DAE-∠CAE，
即∠BAE=∠DAC，
∵∠BAD=100°，∠CAE=40°，
∴∠BAE=
（∠BAD-∠CAE）=
（100°-40°）=30°，
∴∠BAC=∠BAE+∠CAE=30°+40°=70°．
∴∠BAC=∠DAE，
∴∠BAC-∠CAE=∠DAE-∠CAE，
即∠BAE=∠DAC，
∵∠BAD=100°，∠CAE=40°，
∴∠BAE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BAC=∠BAE+∠CAE=30°+40°=70°．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
点重合，AE⊥AB，AE=BD，连接DE、DC．