Question

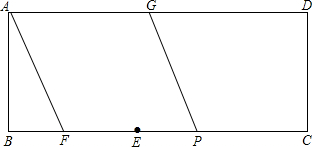矩形ABCD，AD=5，AB=BE=2，点F是BE上的动点，以AF为一边菱形AFPG交BC于P点交AD于G点，如果分别以GP、DC为直径作圆，且使两圆外切，求BF的值．

Answer 1

考点：矩形的性质,菱形的性质,相切两圆的性质

专题：计算题

分析：设BF=x，则AF=

x2+4

，根据四边形AFPG是菱形可以得到FP=PG=AF=AG，由两圆外切的性质和梯形的中位线的性质可以得到PC+DG=PG++CD，进而可以得到关于x的方程，解出即可．

解答：解：设BF=x，则AF=PG=

x2+4

，PC=BC-BF-FP=5-x-

x2+4

，DG=AD-AG=5-

x2+4

，
∵以GP、DC为直径的两圆外切，
∴

1

2

PG+

1

2

CD=

1

2

(PC+DG)，
∴PG+CD=PC+DG，
即

x2+4

+2=5-x-

x2+4

+5-

x2+4

，
解得x=

-2+3 2

2

，
即BF=

-2+3 2

2

．

点评：考查了矩形的性质、菱形的性质、外切两圆的性质、梯形中位线的性质，涉及到的知识点比较多，利用了方程来解答几何题目的思想．