Question

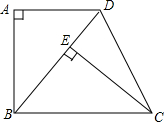如图，已知四边形ABCD是梯形，AD∥BC，∠A=90°，BC=BD，CE⊥BD，垂足为E．
（1）求证：BD=AD+DE；
（2）若∠DBC=50°，求∠DCE的度数．

Answer 1

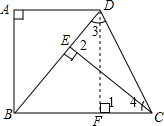（1）证明：过D作DF⊥BC，
又∵CE⊥BD，
∴∠2=∠1=90°，
∵BC=BD，
∴∠3=∠4，
在△DEC和△CFD中，
，
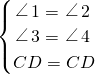∴△DEC≌△CFD（AAS），
∴ED=FC，
∵AD∥BC，
∴∠1=∠ADF=90°，
∵∠A=90°，
∴四边形ABFD是矩形，
∴AD=BF，
∴DB=BF+CF=AD+DE．

（2）解：∵DB=CB，∠DBC=50°，
∴∠3=∠4=（180°-∠DBC）÷2=65°，
∵∠BEC=90°，
∴∠ECB=90°-50°=40°，
∴∠DCE=65°-40°=25°．
分析：（1）过D作DF⊥BC，可证明四边形ABFD是矩形，得到AD=BF，然后再证明△DEC≌△CFD可得ED=FC，再利用等量代换可得结论；
（2）根据等腰三角形的性质计算出∠BCD，然后再根据直角三角形的性质计算出∠ECB，再利用角之间的和差关系可得答案．
点评：此题主要考查了梯形，以及全等三角形的判定与性质，等腰三角形的性质，关键是正确做出辅助线，得到矩形ABFD．