题目内容
已知△ABC是⊙O的内接正三角形,△ABC的面积等于a,DEFG是半圆O的内接正方形,面积等于b, 的值为
的值为
- A.2
- B.

- C.
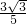
- D.

D
分析:根据圆内接正三角形的性质以及正方形的性质分别用圆的半径表示出两图形面积,即可得出答案.
解答: 解:连接OG,CO,过点O作OM⊥BC于点M,
解:连接OG,CO,过点O作OM⊥BC于点M,
设⊙O的半径为r,
∵△ABC是⊙O的内接正三角形,
∴∠OCM=30°,
∴OM= CO=
CO= r,CM=
r,CM= r,
r,
∴△ABC的高的长度为: r,
r,
BC= r,
r,
∴a= ×
× r×
r× r=
r= r2,
r2,
设正方形DEFG的边长为:x,
则OF= ,
,
∴r2=x2+( )2,
)2,
解得:x2= r2,
r2,
∴b= r2,
r2,
∴ =
= =
= .
.
故选:D.
点评:此题主要考查了正多边形和圆的有关计算,根据圆内接正三角形的性质用圆的半径表示出三角形面积是解题关键.
分析:根据圆内接正三角形的性质以及正方形的性质分别用圆的半径表示出两图形面积,即可得出答案.
解答:
 解:连接OG,CO,过点O作OM⊥BC于点M,
解:连接OG,CO,过点O作OM⊥BC于点M,设⊙O的半径为r,
∵△ABC是⊙O的内接正三角形,
∴∠OCM=30°,
∴OM=
 CO=
CO= r,CM=
r,CM= r,
r,∴△ABC的高的长度为:
 r,
r,BC=
 r,
r,∴a=
 ×
× r×
r× r=
r= r2,
r2,设正方形DEFG的边长为:x,
则OF=
 ,
,∴r2=x2+(
 )2,
)2,解得:x2=
 r2,
r2,∴b=
 r2,
r2,∴
 =
= =
= .
.故选:D.
点评:此题主要考查了正多边形和圆的有关计算,根据圆内接正三角形的性质用圆的半径表示出三角形面积是解题关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目

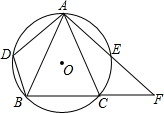 (2012•五通桥区模拟)如图,已知△ABC是⊙O的内接三角形,AB=AC,AD=AE,AE的延长线与BC的延长线交于点F.
(2012•五通桥区模拟)如图,已知△ABC是⊙O的内接三角形,AB=AC,AD=AE,AE的延长线与BC的延长线交于点F.