题目内容
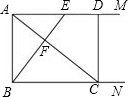如图，射线AM，BN都垂直于线段AB，点E为AM上一点，过点A作BE的垂线AC分别交BE，BN于点F，C，过点C作AM的垂线CD，垂足为D，若CD=CF，则| AE | AD |
分析：由于AD∥BC，易得△AEF∽△CBF，那么AE：BC=AF：FC，因此只需求得AF、FC的比例关系即可．可设AF=a，FC=b；在Rt△ABC中，由射影定理可知AB2=AF•AC，联立CD=CF=AB，即可求得AF、FC的比例关系，由此得解．
解答：解：设AF=a，FC=b；
∵AM⊥AB，BN⊥AB，
∴AM∥BN；
∴△AEF∽△CBF；
∴AE：BC=AF：FC=a：b；
Rt△ABC中，BF⊥AC，由射影定理，得：
AB2=AF•AC=a（a+b）；
∵AM⊥AB，BN⊥AB，CD⊥AM，
∴四边形ABCD是矩形，
∴CD=AB=CF=b；
∴b2=a（a+b），即a2+ab-b2=0，（
）2+（
）-1=0
解得
=
（负值舍去）；
∴
=
=
．
∵AM⊥AB，BN⊥AB，
∴AM∥BN；
∴△AEF∽△CBF；
∴AE：BC=AF：FC=a：b；
Rt△ABC中，BF⊥AC，由射影定理，得：
AB2=AF•AC=a（a+b）；
∵AM⊥AB，BN⊥AB，CD⊥AM，
∴四边形ABCD是矩形，
∴CD=AB=CF=b；
∴b2=a（a+b），即a2+ab-b2=0，（
| a |
| b |
| a |
| b |
解得
| a |
| b |
| ||
| 2 |
∴
| AE |
| AD |
| a |
| b |
| ||
| 2 |
点评：此题主要考查了矩形的性质、直角三角形及相似三角形的性质．能够正确的在Rt△ABC中求得AF、FC的比例关系是解答此题的关键．
练习册系列答案
相关题目
． 
．
．